Le « Big Bang », ta mère (Partie 3)

8 janvier 2015 , par Christophe Delattre

Si vous n’avez pas lu les deux premières parties de cet article, c’est le moment de vous y rendre : Partie 1 – Partie 2.

Troisième étape : Le Big Bang n’est pas une explosion

La vulgarisation est un art délicat mais chaque fois que j’entends parler du Big Bang comme d’une explosion… j’explose ! Et cela arrive bien trop souvent, même dans de bonnes émissions ou revues de vulgarisation scientifique. Employer ce terme d’explosion vous amène inévitablement sur une fausse piste : une explosion de matière au milieu d’un espace vide. Non, le Big Bang n’est pas cela. Lorsque l’on parle d’expansion de l’univers, c’est l’espace lui-même qui est en expansion. Si l’on veut parler d’explosion, c’est l’espace qui explose, pas la matière (et c’est là qu’il est utile d’avoir lu la première partie de ce merveilleux exposé).

Interrogeons nous d’abord sur la « forme » que peut avoir l’univers (oui, je vais encore user de beaucoup de guillemets). Il existe une myriade de modèles « chiffonnés » mais nous allons nous limiter aux « formes » les plus simples correspondant à un univers à « courbure positive », un univers « plat » et un univers à « courbure négative ». On va reprendre un peu tout cela.

Les qualificatifs employés (courbure ou platitude) ne sont que des images, des analogies. Vous vous souvenez que l’espace peut localement s’étirer ou se contracter (c’est dans la partie 1, je n’y reviens pas), ce qui n’est pas sans effet sur la géométrie de l’univers dans son ensemble. Prenons par exemple le triangle que nous dessinerions en reliant trois galaxies très éloignées les unes des autres (tellement éloignées qu’à cette échelle, l’univers puisse sembler homogène… car à l’échelle de votre salon, l’univers l’est moins). Comme tout triangle, on s’attend à ce que la somme de ses angles soit égale à 180° (c’est ce que vous apprenez dans vos premiers cours de géométrie). Mais, en tenant compte de la Relativité générale, il se peut que cette somme soit supérieure à 180° (courbure positive) ou inférieure à 180° (courbure négative).
En fait, et je déflore un peu beaucoup la quatrième partie, la somme des angles est, selon nos observations, égale à 180° dans l’univers observable. Oubliez ce que je viens d’écrire, on verra cela après…

Ca gratouille encore dans les neurones ? Ok, procédons nous aussi par images, par analogie.

Imaginons un univers ne possédant que deux dimensions spatiales, avec des petits bonshommes plats, tels des personnages de BD. Ils vivent sur une terre plate, dans une galaxie plate, errant au milieu de milliards de galaxies plates dans un espace qu’ils pensent plat. Ils connaissent la longueur et la largeur mais la profondeur n’a aucun sens pour eux, pas plus qu’un cube ou une sphère.

Comment pouvons-nous imaginer la forme de leur univers ?

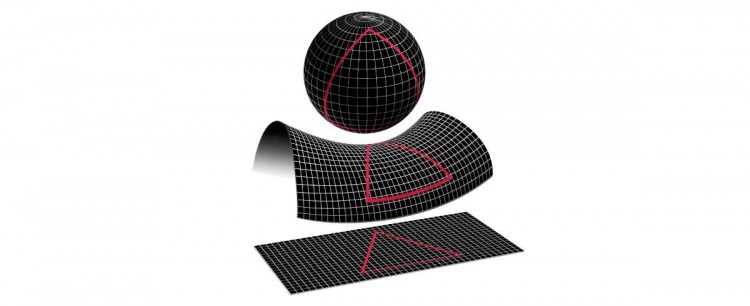
S’il s’agit d’un univers plat, eh bien, leur univers est tout simplement infini et… plat, même si au niveau local, il y a quelques boursouflures dont ils ne se doutent pas mais que leur Albert a deviné en voyant leur terre plate faire des ronds autour de leur soleil plat.

S’il s’agit d’un univers à courbure négative, le modèle le plus simple – si l’on peut dire – est un univers infini en forme de selle de cheval. Vous n’êtes pas féru d’équitation ? Laissons tomber.

S’il s’agit un univers à courbure positive, le modèle le plus simple est une sphère. Leur univers est donc, dans ce cas, fini et sans limite. Cet univers possède bien une surface déterminée (un nombre de mètres carrés si vous préférez) mais ils auront beau le parcourir en long et en large, ils ne trouveront jamais de limite. Mieux : en allant tout droit, ils risquent de revenir sur leurs pas. Mettez-vous bien en tête que ni l’intérieur, ni l’extérieur de cette sphère n’ont de réalité : leur univers n’est que la surface de cette sphère.

A quoi ressemble leur Big Bang ?

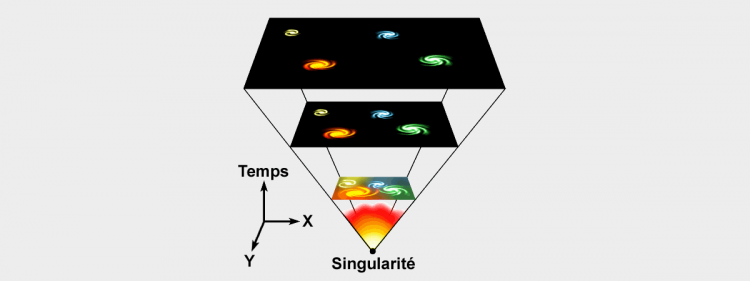
Prenons le dernier exemple : l’univers-sphère. Les astronomes plats se sont rendus compte que leurs galaxies plates s’éloignaient d’eux, et ce d’autant plus vite qu’elles sont éloignées. Un peu comme si leur Terre plate était au centre d’une gigantesque explosion de matière. Mauvaise interprétation. Imaginons leur univers : un gigantesque ballon de baudruche sur lequel serait disposé des milliards de gommettes représentant leurs galaxies. Ce qu’il viennent de découvrir, c’est que leur ballon de baudruche est en train de gonfler !… Imaginez-vous, tout plat, présent au sein de l’une de ses gommettes : vous verriez effectivement toutes les autres gommettes s’éloigner à mesure que le ballon gonfle, et ce d’autant plus vite qu’elles sont éloignées. Et vous n’êtes au centre de rien : quelle que soit la gommette où vous vous trouvez, l’expérience est identique. L’univers n’a pas de centre.

Il est alors possible d’imaginer le passé de cet univers. En repassant le film à l’envers, nous voyons le ballon se dégonfler, les gommettes se rapprocher de plus en plus les une des autres, jusqu’à ce que tout le ballon et ses gommettes se retrouvent concentrés en un point d’une densité « infinie » (on reviendra sur ces guillemets). Ce n’est pas seulement la matière (les gommettes) mais bien tout l’univers (le vide y compris, c’est à dire la surface du ballon) qui se retrouve concentré en un point. Vous l’avez compris, il s’agit là du Big Bang.

Il est bien sûr possible de déterminer le temps écoulé depuis ce Big Bang (13,8 milliards d’années). Vous aurez également compris que la question de savoir en quel endroit de l’univers (en quel endroit de la surface de ce ballon) a eu lieu le Big Bang, n’a pas de sens : il a eu lieu partout puisque tout l’univers était compris dans ce Big Bang !

Et quid du Big Bang si leur univers est infini ?

Prenons alors le premier exemple, celui de l’univers plat et infini. Curieusement, si cet univers semble plus simple à décrire, le Big Bang y est pourtant plus difficile à comprendre, et ce en raison des difficultés que nous avons, vous et moi, à appréhender la notion d’infini.

Il faut imaginer une toile élastique, quasiment plate (si ce n’est quelques boursouflures par ci, par là), s’étendant à l’infini et sur laquelle sont disséminées une infinité de gommettes-galaxies. Là aussi les astronomes plats se rendent compte que les galaxies s’éloignent d’eux, et d’autant plus vite qu’elles sont éloignées.

C’est en fait cette toile infinie (leur espace) qui s’étire de plus en plus au fur et à mesure du temps. Là peut être la difficulté : vous devez comprendre qu’un univers infini peut s’étirer (ou se rétracter) tout en restant bien sûr infini. Il est, là aussi, possible de repasser le film à l’envers : voir cette toile infinie se contracter peu à peu, voir les gommettes se rapprocher les unes des autres jusqu’à atteindre une densité « infinie ». C’est le Big Bang. Mais attention, ici, la densité est infinie en tout point d’un univers qui lui-même reste infini (et non plus réduit à un point comme dans l’exemple précédent). Toutefois, si l’on ne parle que de « l’univers observable » (une notion que nous verrons dans la partie suivante), cet « univers observable » se réduirait bien, lui, à un point.

Et dans notre univers, cela donne quoi ?

Si vous avez réussi à appréhender ce qui précède, sachez que c’est un peu la même chose pour nous.

Si notre univers est infini, il faut imaginer que notre espace est très élastique. Les galaxies s’éloignent de nous parce que l’espace s’étire entre elles et nous, à l’image d’un pudding aux raisins gonflant dans le four. Tous les raisins s’éloignent les uns des autres. Bien sûr, ici, ce pudding (l’espace) est infini, et il contient un nombre infini de raisins (galaxies). Si l’on remonte le film à l’envers, cette infinité de galaxies se rapprochent jusqu’à ce que la matière atteigne un état de densité « infini »… en tous points de cet univers infini. C’est le Big Bang.

Si notre univers est fini, sa géométrie la plus simple correspond à ce que l’on appelle une hyper-sphère. Cet univers possède un volume fini, mais ne possède aucune limite. Cela signifie que si vous partez tout droit (réellement tout droit), vous pourriez revenir par derrière, au même endroit (soyez les bienvenus dans la géométrie non euclidienne !). Ce voyage reste bien sûr une expérience de pensée car l’univers est, au minimum, très très très très très très très très grand. Et si vous ne parvenez pas à appréhender cet univers fini et sans limite, c’est normal : essayez d’expliquer à des petits bonshommes plats que leur univers est une sphère.
Dans ce cadre fini et sans limite, le Big Bang correspond, en remontant le passé, à une contraction de l’espace en un point infini (en fait, une hyper-sphère réduite à un point) et donc de densité « infinie ». Comprenons-nous bien, il ne s’agit pas d’un point de matière infiniment concentré dans un espace vide. C’est l’espace lui-même (avec tout ce qu’il contient) qui se réduit à un point.

Vous comprenez ainsi qu’il y a un peu plus de 13 milliards d’années, le Big Bang a eu lieu partout, que ce « partout » soit infini ou qu’il fut réduit à un point. Et qu’il ne s’agit en rien de l’explosion de matière que pouviez imaginer.

Il reste néanmoins beaucoup de questions, beaucoup d’infinis et sans doute pas assez de physique quantique. Nous y allons…