C’est la plus célèbre équation de la physique : « E=mc² », mais sa signification profonde demeure inconnue, mystérieuse, étrange pour la plupart des personnes. Ce qui sans doute contribue également à son aura. Nous allons essayer ici de la démystifier… ce qui, au final, ne la rendra pas moins belle. Bien au contraire.
A ce stade du récit, nous sommes à la fin du mois de septembre 1905. Mais si vous êtes arrivé directement ici, pensez à faire un tour dans le passé, qu’il s’agisse de l’antiquité, de la renaissance ou du XIXe siècle, ou encore il y a trois mois, en juin de cette même année.
Au tour de la masse et de l’énergie
Nous sommes donc le 27 septembre 1905, date d’envoi du dernier article de l’année « miraculeuse ». Il s’agit de quelques feuillets venant compléter l’article de juin. Durant l’été, notre ami Einstein s’interroge en effet sur les conséquences de sa théorie de la Relativité vis-à-vis d’autres concepts physiques que le temps et l’espace, à savoir les notions de masse et d’énergie : deux concepts qui, pour la Mécanique de Newton, demeuraient totalement indépendants l’un de l’autre.
Même si, dans l’article précédent, on vous a chatouillé les neurones avec le temps et l’espace, vous saviez de quoi il s’agissait. En revanche, pour la masse et l’énergie, il y a peut-être besoin de préciser un peu les choses, en essayant de rester concis...
On associe souvent la masse à une grandeur en kg, représentant la quantité de matière que possède un corps (et pas uniquement votre corps de rêve). En physique, elle correspond à deux choses a priori différentes : la « masse grave » (ou « pesante » ou « gravitationnelle »), représentant l’intensité avec laquelle un corps est soumis à la gravitation, et la « masse inerte » (ou « inertielle ») qui mesure la difficulté que l’on a à modifier le mouvement d’un corps (à le mettre en mouvement, à l’accélérer, à le freiner). Il se trouve que ces deux masses sont absolument équivalentes. Et en 1905, comme du temps de Newton, on ne sait pas pourquoi il en est ainsi. Quelques années plus tard, une réponse viendra (devinez par qui ?)… mais là n’est pas encore la question pour Albert. Sachez simplement que la masse dont nous parlerons ici, est la masse inerte.
Quant à l’énergie, il a fallu attendre le XIXe siècle pour lui trouver son actuelle définition. Et là, je laisse parler Wikipedia : l’énergie est une mesure (en joules) de la capacité d’un système à modifier un état, à produire un travail entraînant un mouvement, un rayonnement électromagnétique ou de la chaleur. C’est en fait beaucoup plus abstrait que vous ne le croyez : ce que vous appelez « consommation d’énergie » n’est ainsi qu’une « transformation d’énergie avec augmentation de l’entropie du système ». Restons-en là, on en parlera mieux une autre fois. Gardez simplement à l’esprit que l’énergie ne disparaît pas. Elle s’échange ou se conserve mais ne disparaît jamais. C’est dans l’essence même de sa définition.
Et c’est justement ce principe de conservation de l’énergie, associé à la relativité du mouvement, qui va amener Einstein à découvrir quelque chose d’assez étonnant, pour ne pas dire détonnant.
L’équation
Dans son article, le jeune fonctionnaire de Berne prend l’exemple d’un objet rayonnant se déplaçant (mouvement rectiligne uniforme) par rapport à l’observateur. Notez, à ce sujet, que toute matière émet continuellement de la lumière dont la fréquence est fonction de sa température. Par exemple, si vous êtes encore vivant, derrière votre écran, vous émettez dans l’infrarouge. Fermons la parenthèse.
A la suite d’un calcul que je vous épargne mais que les plus téméraires pourront suivre sur la vidéo ci-dessous (en anglais avec sous-titres Youtube), il conclut que ce rayonnement fait obligatoirement perdre à l’objet une masse correspondant à l’énergie de ce rayonnement lumineux divisé par c². Il n’écrit pas « E=mc² » mais c’est pourtant bien ce qu’il vient de dire.
Il affinera la chose en 1907, et livrera d’autres démonstrations dans les années suivantes. L’équation décrivant l’énergie d’un objet (ayant une masse) en mouvement est alors la suivante :
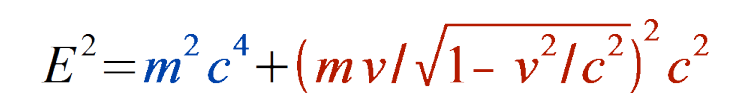
Oui, ça fait un peu long sur un tee-shirt. Veuillez noter que E=mc² est à nouveau inclus dans cette équation : c’est ce que vous obtenez si l’objet est immobile par rapport à l’observateur.
Mais si, regardez : si la vitesse est nulle (v=0), la partie rouge disparaît et, par simplification, vous obtenez E=mc².
Bon, pour vous faire plaisir, je vous confirme qu’il finira par écrire explicitement « E=mc² » dans quelques textes, quelques années plus tard (je le mettrai plus bas). Mais là n’est pas le vrai sujet. A ce stade, vous avez des chiffres, des lettres, des signes mais… si vous n’êtes qu’un honorable béotien, vous continuez à regarder cette équation avec des yeux ronds, mi-curieux, mi-dubitatifs. La question demeure : que nous dit réellement cette équation ?
Derrière l’équation
Jusque là, vous avez peut-être compris que, dans « E=mc² », le E concerne une énergie, et qu’il y aurait une équivalence avec une masse m si on la multiplie par un facteur égal à c au carré… Certes…
Pour dire la vérité, ce n’est pas tant l’équation « E=mc² » elle-même qui est révolutionnaire. D’autres qu’Einstein l’ont écrite dans les années précédentes pour expliquer d’autres choses et dans un autre contexte. Nous y reviendrons… Plus que dans l’équation elle-même, c’est dans la manière dont il arrive à ce résultat, dans la signification qu’il en donne et dans les conclusions qu’il en tire que se situe le véritable génie d’Einstein.
Découvrons enfin ce qui se dissimule derrière cette équation…
De la masse disparaît
Vous avez sûrement appris à l’école que rien ne se perd, tout se transforme. C’est ainsi que parlait Lavoisier, le Père de la chimie moderne, avant qu’il se fasse couper la tête en 1794. En gros, cela signifie que si vous utilisez 1 kg de ceci et 1 kg de cela pour faire une réaction chimique, vous obtiendrez 2 kg d’autres choses. Bref, la masse se conserve.
Et là, en 1905, Einstein nous dit que si un objet perd de l’énergie en émettant de la lumière (qui n’a pas de masse), alors cet objet perdra de la masse. Je répète : un objet perd de la masse en émettant quelque chose qui n’a pas de masse. Il vient tout simplement de fouler aux pieds le principe de conservation de la masse.
Sur la piste de « c »
Si l’objet en déplacement ne possède pas de masse (m=0), ce qui est dans la parenthèse rouge (que l’on nomme l’impulsion) s’écrit un peu autrement. Je vous passe la démonstration (à voir sur Wikipedia si vous le souhaitez) mais sachez que l’on obtient alors « v=c ». De même, si l’on part de « v=c », on obtient « m=0 ».
En termes plus familiers… Si une particule possède une masse nulle, elle ne connaîtra jamais le repos. Sa vitesse sera « c », et sera toujours « c » quel que soit notre point d’observation. Et, de même, si quelque chose va à la vitesse c, c’est que sa masse est nulle.
Je m’étais un peu précipité dans le précédent article mais c’est ici que l’on comprend que la vitesse « c » n’est pas une propriété particulière de la lumière. La lumière se déplace à la vitesse « c » parce que la lumière n’a pas de masse. Et ce sera le cas pour toute autre particule qui n’aurait pas de masse. Il est donc restrictif de dire que « c » est le nom pour « la vitesse de la lumière ». « c » est plus que ça. Et même bien plus, ainsi que nous allons le voir…
La nature de « c »
« c » qui n’était que la vitesse particulière d’un phénomène particulier : la lumière, est à présent la vitesse obligatoire de toutes particules sans masse. Mais ce n’est pas fini… Einstein comprend que son équation demeure valable quel que soit le processus par lequel l’objet perd de l’énergie, c’est à dire même si ce processus ne fait pas intervenir de lumière ou de quelconques particules sans masse. Et même dans ce cas, même quand il n’y a plus de lumière, « c » demeure dans l’équation.
Cela veut donc dire que « c » est plus que la vitesse d’objets de masse nulle. C’est une constante (ayant la forme d’une vitesse) qui gouverne les lois de l’univers. C’est ce que l’on appelle une constante fondamentale. Par convention, on continuera à la nommer « vitesse de la lumière » mais vous comprenez à présent que c’est un tantinet réducteur.
Les fondations du mur
Nous avions expliqué pourquoi « c » était un mur, une vitesse inatteignable pour tout corps massif (l’exemple de la fusée dans l’article précédent). Cela apparaît de nouveau dans l’équation. En effet, plus v (la vitesse de l’objet) s’approche de c, plus la partie rouge (et donc l’ensemble de l’énergie) tend vers l’infini.

Dit autrement, ce que nous révèle cette équation, c’est que si un objet se déplace par rapport à nous (ultra vite pour que l’effet puisse être tangible), nous observerions non seulement que sa longueur se contracte et que son temps se dilate, mais aussi que sa masse augmente (notez que le m de l’équation correspond à la masse au repos)… Et plus cette masse augmente, plus il faudra d’énergie pour le faire avancer encore plus vite. Et tout ceci de manière exponentielle. A l’extrême, il faudrait une énergie infinie (réellement infinie) à la fusée, dont la masse deviendrait infinie (réellement infinie), pour que l’on puisse la voir s’éloigner de nous à la vitesse de la lumière. Nous revoilà dans le mur.
Précisons encore une fois que cet effet, comme tous les autres, demeure microscopique, insignifiant, tant que la vitesse de déplacement en question demeure petite par rapport à c. Si une voiture consomme plus de carburant pour accélérer de 110 à 130 km/h, que pour passer de 10 à 30 km/h, c’est dû à la résistance de l’air et au frottement des pneus, et non à un quelconque effet relativiste.
L’un des secrets de la matière
Vous vous doutez bien que j’ai gardé le meilleur pour la fin…
Pour faciliter l’explication, je vous fournis ci-dessous l’équation donnant l’énergie d’un objet (de masse non nulle) en mouvement, sous une autre forme… D’abord de la main d’Einstein (je vous l’avais promis) :
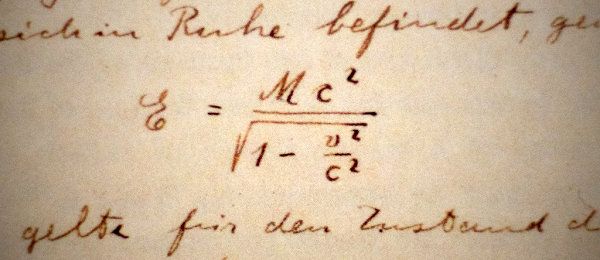
Puis avec un développement en série entière de la fonction (pas grave si c’est du chinois pour vous) :
Si la partie rouge de cette équation représente l’énergie cinétique de la physique classique passée à la moulinette relativiste, la partie bleue n’a, elle, aucune contre-partie chez Newton. C’est quelque chose de nouveau, et qui demeure seul dans la partie droite lorsque l’objet est au repos (v=0), l’équation correspondant alors au fameux E=mc². Cette partie bleue (mc²) est apparue pour assurer la conservation de l’énergie dans un cadre relativiste. Mais que peut-elle signifier ?
Pour Einstein, ce n’est pas un artifice mathématique. Il y a là quelque chose que la nature nous avait dissimulé. Et c’est énorme !
Énorme d’abord par l’énergie que cela représente.
Prenons l’exemple d’une feuille de papier A4 de bonne qualité. Vous la roulez en boule, la tenez haut dans une main, et vous la faites tomber dans l’autre main. D’une certaine manière, vous venez de ressentir dans la paume de votre main, l’énergie qui est en jeu dans la partie rouge de l’équation, c’est à dire l’énergie cinétique de la boule de papier en mouvement (soit 1/2 de mv², comme on vous l’a appris à l’école, les autres termes rouges étant quasi nuls du fait de la petitesse de v par rapport à c).
Quant à savoir ce que représente la partie bleue de l’équation (le mc²), toujours concernant cette boule de papier (c’est à dire ce qu’il reste de l’énergie de la boule de papier, une fois qu’elle est au repos) ?… C’est simple : huit fois la bombe d’Hiroshima !
Oui, numériquement, c’est cela « E=mc² » : E, l’énergie au repos de la boule de papier (en joules), égale à la masse de la boule de papier (en kg) multipliée par une constante faramineuse, c au carré (en m²/s²).
Ok, « mc² » représente quelque chose d’énoOorme… Mais quel est le sens profond de l’équation « E=mc² » ?
Elle établit une équivalence entre l’énergie et la masse, deux concepts qui étaient étrangers l’un à l’autre chez Newton (on peut même parler d’égalité si l’on utilise des unités relativistes plutôt que les joules et les grammes). Et Einstein comprend – et il est le premier à le comprendre – que, par cette équation, il vient de soulever un voile dissimulant la nature intime de ce que l’on nomme la matière. Et il confie d’ailleurs à la fin de son papier de septembre 1905 que la « récente » découverte (par Marie Curie) de l’activité des sels de radium (qui aboutira à la découverte de la radioactivité) pourrait être en mesure de confirmer cela (et bien sûr il a mis dans le mille !).
Oui, depuis septembre 1905, ce que l’on appelle la matière s’apparente… à de l’énergie cristallisée. Une gigantesquissime réserve d’énergie cristallisée.
En arborant « E=mc² » sur votre tee-shirt, c’est un peu du secret de l’Univers que vous dévoilez à la face du Monde.
E = mc² à l’œuvre
Pour mieux comprendre ce dernier point, voyons concrètement de quoi il peut s’agir…
De la matière, naît l’énergie
Comme Albert Einstein l’avait pressenti, c’est au sein des phénomènes nucléaires que E=mc² va, pour la première fois être mis en évidence. Ce sera en 1932, avec l’énergie « consommée » par la fission d’atomes de lithium. Je vais toutefois prendre d’autres exemples, plus parlants…
Allons au marché aux atomes… Choisissons un bel atome d’uranium 235, faisant une masse d’1kg (en réalité, c’est 0,0000000000000000000000004kg mais faisons comme-ci pour nous simplifier la tâche). Plaçons notre atome d’1kg sur la table et tapons dessus avec une bille (un neutron). Comme on pouvait s’en douter, il se casse en plusieurs morceaux (atomes plus légers et neutrons). « Pesons » ces morceaux… On obtient 0,9992kg ! Il manque donc 0,8g. Que sont devenus ces 0,8g ? Ils n’existent plus. Ou, pour être plus précis, ils se sont transformés en énergie. Une énergie E égale à la masse perdue multipliée par c au carré. Concrètement, ces 0,8g se sont transformés en… vitesse (la vitesse acquise par les morceaux issus de la fission de l’atome d’uranium).
C’est ce qui se passe dans les bombes A et les centrales nucléaires : on transforme de la matière en vitesse.
On peut poursuivre nos courses, et acheter deux petits atomes de deutérium (c’est une variété très onctueuse d’hydrogène). Chaque atome de deutérium pèse 1g (en vrai, c’est fichtrement moins mais, encore une fois, c’est pour l’exemple). Vous prenez vos deux deutérium d’1g, et vous les coller ensemble, histoire de fabriquer un magnifique atome d’hélium. On pourrait s’attendre à ce que cet atome d’hélium « pèse » 2g. Mais vous l’avez compris, ce n’est pas le cas : c’est moins que 2g. Et la masse perdue s’est à nouveau transformée en énergie, en suivant l’équation E=mc².
Cette fusion de l’hydrogène, c’est ce qui se passe dans les bombes H mais aussi au cœur du Soleil : chaque seconde, notre étoile transforme près de 619 millions de tonnes d’hydrogène en 614 millions de tonnes d’hélium. Chaque seconde, au cœur du Soleil, 4,26 millions de tonnes de matière disparaissent, transformées en énergie pour, entre autres, vous permettre de bronzer sur la plage.

Si la fission d’atomes lourds ou la fusion d’atomes légers (réactions nucléaires) produisent une énergie issue d’une perte de masse, qu’en est-il des simples réactions chimiques ? Contrairement à ce que pouvait penser Lavoisier (et peut-être même votre prof de chimie), l’énergie d’une réaction chimique est bel et bien issue du même mécanisme, de la même équation E=mc². La combustion explosive de l’hydrogène avec l’oxygène donne de l’eau. Mais l’eau obtenue a une masse inférieure à celle des produits du départ. Un petit bémol toutefois : la masse perdue ne correspond qu’à un dix millième de milliardième de la masse d’origine !… C’est trop infime pour être décelé, et c’est pourquoi la tête de Lavoisier ne se retourne pas dans sa tombe.
Reprenons… Dans chaque gramme de matière (et peu importe la matière : or, pétrole, air, caillou, poils de shih-tzu,…) se dissimule une énergie supérieure à celle libérée par la bombe d’Hiroshima.
Par la chimie, on parvient à extraire de ce gramme de matière, un microscopique chouia d’énergie. Avec la fission nucléaire d’éléments lourds, on fait beaucoup mieux. Et encore un peu mieux avec la fusion nucléaire d’éléments légers. Mais cela reste néanmoins ridicule par rapport à ce que représente l’énergie contenue dans ce gramme de matière. Une question se pose donc : est-il possible de libérer toute cette énergie ?
La réponse est oui, et la solution s’appelle… l’antimatière (encore un article en perspective). Si une particule de matière (un électron par exemple) rencontre son antiparticule (un positon), que se racontent-ils ? Des histoires d’énergie !
En effet, la rencontre d’un électron et d’un positon (chacun possédant la même masse) aboutit à leur annihilation : ils disparaissent, avec leur masse, ne laissant derrière eux qu’un grand éclair de lumière (un rayonnement gamma pour être précis) dont l’énergie correspond bien à leur masse multipliées par c au carré. Comme rendement, on ne peut pas faire mieux… Mais calmez-vous, ce n’est malheureusement pas demain que votre voiture roulera à l’antimatière avec des poils et des anti-poils de shih-tzu.
Voilà. Nous venons de voir comment la masse pouvait se transformer en énergie, en suivant l’équation E=mc². Qu’en est-il du processus inverse ?
De l’énergie, naît la matière
« E=mc² » peut également s’écrire « m=E/c² ». Cela signifie t-il que l’on peut créer de la matière à partir de l’énergie ? Tout à fait… Bien sûr, le fait que le c² soit ici au dénominateur, implique qu’il faille une énergie colossale pour ne créer que de modestes particules, sans compter que pour créer une particule massive, il faut, en même temps, créer son antiparticule afin que le bilan des charges reste neutre, ce qui augmente d’autant l’énergie nécessaire.
Un rayonnement gamma (la lumière la plus énergétique qui soit) peut aboutir à cette création de paires particule-antiparticule mais l’exemple le plus courant que l’on puisse donner concerne les accélérateurs de particules.
Prenez le LHC du Cern à Genève qui fait se heurter des protons et des anti-protons à ultra haute vitesse (on est très près de c). Contrairement à ce que beaucoup pensent, il ne s’agit pas ici de « casser » des particules pour voir ce qu’il y a l’intérieur. Non, le but est de créer une colossale densité d’énergie (l’énergie cinétique des protons et anti-protons) concentrée en un point (dans un détecteur) afin que, de cette énergie, naissent de nouvelles particules.
Concrètement, disons qu’au repos, le proton, tout comme l’anti-proton, fait un gramme (c’est bien sûr astronomiquement moins, mais c’est à nouveau pour la clarté de l’explication). Faisons-les se taper dessus à ultra haute vitesse. Du choc, jaillit une gerbe de particules diverses et variées (voir un exemple ci-dessus), et si vous additionnez la masse de toutes ces particules qui n’existaient pas avant le choc, vous obtenez des centaines, voire des milliers de grammes. De la matière a été créée !
Et il faut bien comprendre pourquoi cela peut paraître extraordinaire. Ici, c’est bien la propriété d’une chose (sa vitesse) qui crée, elle-même, d’autres choses ! Pour reprendre des exemples donnés par le physicien Etienne Klein, c’est aussi incroyable que de dire que la « hauteur » de la Tour Eiffel pourrait engendrer un immeuble. Ou, plus en rapport, que la « vitesse » d’un taxi pourrait créer un scooter, voire un autobus !
Oui, le « E=mc² » d’Einstein est impressionnant, déroutant, presque « magique »… mais maintenant, vous savez pourquoi !
Controverses concernant E = mc²
Parce qu’il faut bien y passer…
La controverse « Poincaré »
Il me faut indiquer qu’il existe une controverse concernant la paternité de cette équation, et plus généralement de la relativité restreinte. Que cette controverse soit née d’intentions louables (analyse scientifique – erronée selon moi et bien d’autres – des travaux en question) ou de mauvaises raisons (nationalisme, antisémitisme ou conspirationnisme), elle tend à attribuer à Henri Poincaré les théories dont nous venons de parler. Précisons que – même si un premier livre l’aborde en 1953 – cette controverse a pris corps assez récemment, et n’est pas du tout le fait d’Henri Poincaré qui jusqu’à sa mort, en 1912, n’a jamais pris à son compte les raisonnements d’Albert Einstein, et semble même avoir eu beaucoup de réticences vis-à-vis d’eux. Henri Poincaré serait sans doute le premier étonné de s’en voir attribué la paternité, même s’il est évident que les travaux du physicien français furent une grande source d’inspiration pour le jeune homme de Berne.
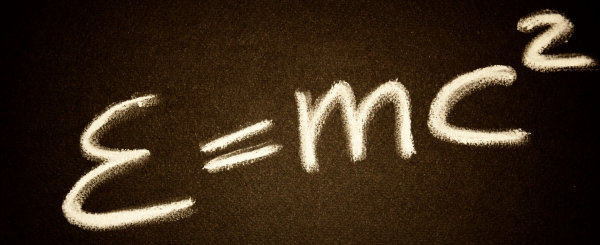
L’exemple de « E=mc² » est assez emblématique. On trouve effectivement cette formule dans un article de Poincaré datant de 1900 (sous la forme « m=E/c² »). Il y explique qu’un rayonnement peut être considéré comme un fluide fictif possédant une masse équivalente à E/c². Le propos est totalement différent chez Einstein, bien plus fondamental, et lui seul implique une révolution de la pensée concernant les notions d’énergie et de matière. Il n’en reste pas moins que la contribution d’Henri Poincaré a longtemps été sous-estimée. De là en faire le véritable auteur des théories d’Einstein ? Non. Et, même si je n’ai pas le bagage historique, physique et mathématique pour me mêler concrètement au débat, je préfère me ranger à l’avis de la très grande majorité des physiciens et historiens des sciences plutôt qu’à celui d’un Claude Allègre (et on parlera aussi du climat, un de ces jours).
La controverse « champignon atomique »
Un malentendu qui a la vie longue, associe « E=mc² » à la bombe atomique. Alors certes, l’énergie qui est ici à l’œuvre correspond bien à la formule d’Albert (à l’image de l’exemple que j’ai utilisé précédemment). Mais il faut bien comprendre que cette formule, dans sa version complète, intervient tout aussi bien dans le lancement d’une sagaie (ou d’un Petit suisse à la cantine). En fait, le développement de cette bombe A puis de sa petite « grande » sœur, la bombe H, ne doit pas grand chose à « E=mc² ». A la limite, on aurait pu fabriquer une telle bombe sans connaître la formule, et la retrouver par l’expérimentation. La fabrication elle-même ne requiert que la physique de Newton et un peu de mécanique quantique. Concrètement, la Relativité ici ne sert à rien, sinon à donner un cadre théorique permettant d’expliquer ce qui se passe.
En réalité, si l’histoire de la bombe atomique ne débute qu’à l’aube de la seconde guerre mondiale, c’est que sa conception doit tout, en fait, à la découverte en 1938 de la fission induite de certains atomes d’uranium (voir ici). Certains comprendront que cela ouvre la possibilité de créer une bombe d’une puissance colossale. Parmi eux, un physicien hongrois, Leo Szilard qui a fui aux USA – comme Einstein – les persécutions antisémites en Europe. Conscient de la possibilité pour l’Allemagne nazie de travailler à cette bombe, c’est lui qui incitera Albert Einstein à user de sa notoriété pour signer, en août 1939, une lettre au président Roosevelt afin de le mettre en garde face à cette menace. Ceci conduira au lancement du projet Manhattan qui, contrairement à son équivalent allemand, se concrétisera, comme on le sait, à Hiroshima et Nagasaki.
La seule responsabilité d’Albert Einstein en ce domaine, concerne donc cette lettre de 1939. On ne peut bien sûr la comprendre qu’en se plaçant dans le contexte dans lequel elle fut écrite : le danger était alors réel de voir Hitler développer la bombe atomique avant les (futurs) alliés, et on pouvait imaginer le cauchemar que cela aurait impliqué. Mais, dès la chute du IIIe Reich, Einstein militera – tout comme Szilard – pour la non-utilisation de l’arsenal nucléaire (ils créeront ensemble le Comité d’urgence des scientifiques atomistes). Il demeurera un farouche militant pacifiste jusqu’à sa mort.
Après la Relativité restreinte
De mars à septembre 1905, Albert Einstein a révolutionné des pans entiers de la physique. Il n’a pourtant pas encore écrit ce qui sera son chef d’œuvre, et qui bouleversera totalement notre compréhension de l’univers. Cette fois-ci, il mettra plusieurs années pour y parvenir, et ce travail s’inscrira dans la lignée de ses deux derniers articles de juin et septembre 1905. Ces deux articles que nous venons d’étudier prendront alors le nom de « Théorie de la relativité restreinte ».
Car, en 1915… naîtra la « Théorie de la relativité générale ».
La relativité
- Partie 1 : ce n’est pas absolu
- Partie 2 : c’est l’égalité
- Partie 3 : ça se contracte
- Partie 4 : c’est révolutionnaire
- Partie 5 : c’est aussi « E= mc² »
- Partie 6 : c’est général
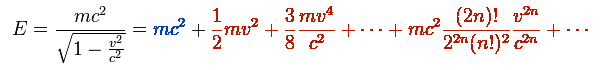







Une belle explication, bravo !
Un petit bémol, dans la vidéo en anglais avec le chat radioactif, j’ai nettement l’impression d’assister à une explication tautologique : E= mc2 parce que E = mc2.
Il faut être attentif au fait qu’à la neuvième seconde de cette vidéo une petite image nous signale qu’on est dans un espace de Minkowski.
J’ai toujours eu du mal avec les explications qu’on donne généralement sur la relativité. Celle-ci découle évidemment de la loi de Lorentz et des recherches de Poincarré mais surtout de la création d’un espace mathématique particulier.
J’ai aussi un problème avec la notion de masse relativiste et préfère de loin la définition de Poincarré.
Dans un espace euclidien, en mécanique newtonienne, la relativité est absolument incompréhensible, Selon moi, elle ne peut se justifier que dans un espace de Minkowski.
Dans un espace euclidien par exemple le paradoxe des jumeaux ne peut pas exister. Si cela vous intéresse, je peux vous en donner la démonstration.
Encore félicitation pour votre site.
Bonjour,
J’accompagne le précèdant commentaire et vous félicite pour la qualité de l’article. Un véritable plaisir des neurones 🙂
Une question me taraude l’esprit dans votre raisonnement, je n’arrive pas à appréhender une réalité, j’espère que vous saurez y répondre. Si pour accélérer un objet (voiture) de 0 à 100 km/h, il faut 4 unités d’énergie, alors pour la faire passer de 0 à 200 km/h, il en faut 16, car l’énergie se calcule avec le carré de la vitesse. Donc pour passer de 100 à 200 km/h, il faut 3 fois plus d’énergie (essence, quantitée mesurable ou palpable je dirais) que pour passer de 0 à 100 km/h. On néglige tous les frottements évidemment).
J’ai séché pas mal de collègues scientifiques avec cette question toute simple. Je n’arrive pas à appréhender la réalité des choses la derrière. Il y a une histoire de relativité des vitesses (référentiel) mais comment la voiture « sait » qu’elle part de 0 ou de 100 km/h, de plus le mouvement n’est comme rien, toujours relative alors que la consommation est réelle.
On pourrait se poser la question pour une fusée dans l’espace, qu’est ce qui définit sa consommation d’énergie pour se propulser sachant qu’elle peut être à n’importe qu’elle vitesse en 0 et C en fonction du référentiel. Encore une fois, le mouvement n’est comme rien, seule l’accélèration consomme de l’énergie.
Merci par avance.
Merci pour les compliments.
Concernant votre raisonnement, l’erreur se situe là : « l’énergie se calcule avec le carré de la vitesse ».
Faisons simple.
Par rapport au piéton, la masse en mouvement de la voiture augmente en fonction de la vitesse de cette voiture (et de ce fait, plus la masse augmente, plus l’énergie nécessaire pour accélérer, augmente).
Pour calculer cette augmentation de masse, vous avez une formule avec au dénominateur la racine carrée de : 1 – (v²/c²).
Si v (la vitesse du véhicule) n’est pas proche de c (la vitesse de la lumière), v²/c² tend vers 0. Le dénominateur est donc égal à 1–0, donc 1, donc rien ne change.
Dit autrement, la masse du véhicule, qu’il roule devant vous à 1km/h, 100km/h ou 200km/h, ne change pas (sinon d’un milliardième de milliardième… etc. de milliardième de gramme).
Donc, hors frottements, il faut la même quantité d’essence pour passer de 0 à 100km/h ou de 100 à 200km/h.
En revanche dès que v va se rapprocher de c, v²/c² va tendre vers 1, et donc 1 – (v²/c²) va tendre vers 0, ce qui fait que la masse tendra vers l’infini (et le nombre de litres d’essence nécessaire aussi).
Bref, pour une voiture (et même une sonde interplanétaire), les effets relativistes sont hautement négligeables (on utilise la mécanique de Newton).
Votre erreur était donc de dire que le calcul s’effectuait en fonction de v² (ce qui est vrai mais insuffisant). Le calcul doit se faire avec « 1 – v²/c² », ce qui change tout car peu importe que v soit égale à 10 ou 10000 km/h, le résultat de « 1 – v²/c² » sera toujours égal à 1 (à un pouillème près).
J’espère avoir bien répondu à l’interrogation 😉
Merci beaucoup de votre réponse travaillée. Cependant, j’avais bien appréhendé le fait que cela n’avait pas avoir avec la théorie de la relativité d’Einsten.
J’ai due mal exprimer mon interrogation. Ce qui me dérange c’est que le mouvement, et donc l’énergie cinétique est relative au référentiel. En reprenant un exemple concret, une voiture qui fonce sur un mur fixe va dégager 4 fois plus d’énergie dans un crash à 200 km/h comparé à un crash à 100 km/h (lénergie cinétique étant au carré de la vitesse). Le référentiel étant dans notre cas le même, le mur fixe.
Dans ce contexte, comment l’énergie nécessaire pour passer de 0 à 100 peut être la même que pour passer de 100 à 200 km/h? Sinon, on récupère plus d’énergie à l’impact qu’à l’accélération, ce qui viole le principe de la thermodynamique et ce n’est pas possible. Où diable ce situe mon erreur?
Merci par avance.
Désolé d’avoir mal compris la question. Et cette question est très bonne !
Je pense avoir la réponse mais je vais devoir vérifier (et demander conseils).
Restez à l’affût…
Me revoilà (et je confirme que la question est bien plus complexe qu’il n’y paraît)..
Donc, comme je le pensais, pour faire un bilan énergétique, il faut prendre en compte l’ensemble du système : accélérer en voiture fait également accélérer la Terre dans l’autre sens (bon, vu la différence de masses…) et l’aspect “élastique des choses”, cela revient surtout à de l’énergie thermique. Dès lors, le paradoxe disparaît.
Si l’on parle d’une voiture, le système isolé est constitué de la Terre (qui n’a rien d’un solide parfait et homogène) et de tout ce qu’il y a dessus (et encore en omettant l’influence gravitationnelle des autres astres).
Enfin bref, pour étudier proprement le problème, on va simplifier les choses au maximum.
Je me situe dans l’espace interstellaire, constituant un repère inertiel à partir duquel nous allons évaluer toutes les vitesses et effectuer tous les calculs.
Nous allons faire le bilan énergétique, avant et après accélération, de deux fusées, l’une passant de v=0 à 10, l’autre passant de v=100 à 110.
Il n’y a aucun frottement et l’on reste dans un cadre classique (pas de vitesse relativiste).
On voit tout de suite le paradoxe apparaître en calculant l’énergie cinétique gagnée par chacune des fusées (on considère que 1/2m fusée = 1) :
Cas 1 (v=0 à 10) ► Ec_final – Ec_initial = 100-0 = 100
Cas 2 (v=100 à 110) ► Ec_final – Ec_initial = 12100-10000 = 2100
Sacrée différence en gain d’énergie pour une même accélération !
Lorsque j’ai posé le problème à des “experts” en physique, beaucoup se sont contentés de redémontrer la loi de l’énergie cinétique, prouvant que Ec=1/2mv² (ce qui n’est pas le problème car personne n’en doute), que le calcul de l’Ec dépend du référentiel (oui, et alors ?).
Bien sûr, il fallait prendre en compte l’énergie qui a permis cette accélération (le carburant) et la plupart ont conclu qu’il fallait plus de carburant pour passer de v=100 à 110 plutôt que de v=0 à 10.
Là, Galilée se retourne dans sa tombe, et je sors de mon chapeau, ce cas pratique :
Je me nomme Arthur, et je suis dans le référentiel inertiel A.
Une fusée B, pilotée par Bernard, est immobile devant moi mais va accélérer sur ma droite de v=0 à 10 en utilisant 1 litre de carburant.
Une fusée C, pilotée par Charles, est déjà partie sur ma gauche depuis un certain temps. Les moteurs sont à présent coupés et elle s’éloigne, sur ma gauche, à une vitesse constante v=100. Elle constitue donc, elle aussi, un parfait référentiel inertiel.
Je calcule le gain en Ec de la fusée B, avant et après l’accélération. Je trouve 100.
Charles fait de même depuis son référentiel, et il trouve 2100.
S’il faut un litre de carburant pour un gain de 100, Charles en conclut donc que Bernard a utilisé 21 litres de carburant. Ce qui expliquerait tout.
Or non, pour moi, pour Charles et pour l’univers entier, Bernard n’a effectivement utilisé qu’un seul litre de carburant. C’est un fait. L’explication ne se trouve donc pas là.
Si vous doutiez qu’une même accélération utilisait le même volume de carburant quelque soit la vitesse initiale, voilà la réponse.
Bien sûr, c’est un cas idéalisé. Ce n’est pas une voiture sur une autoroute qui va devoir lutter contre le frottement de l’air à mesure que la vitesse augmente.
Mais cela n’explique pas comment résoudre le paradoxe ? On vient juste de réfuter une réponse possible.
On reprend le problème du départ, de manière correcte…
____________________
J’observe depuis un référentiel inertiel dans l’espace interstellaire, et je tente de calculer le bilan énergétique d’un système isolé (fusée + éléments de propulsion).
Puisqu’il y a conservation de l’énergie du système (système isolé, calculs à partir d’un référentiel inertiel, moi), on a :
Somme des énergies cinétique et potentielle initiales = Somme des énergies cinétique et potentiel finales.
C’est ce bilan que l’on va faire dans ces deux cas (vi=0 et vi=100), avant et après l’accélération.
Tous les calculs se font dans mon référentiel (et non celui de la fusée), y compris la vitesse des gaz ce qui fait, bien sûr, que leur énergie cinétique est différente dans les deux cas (avec un différentiel de vitesse égal à 100 entre les deux cas).
On peut simplifier la propulsion en prenant (au lieu du carburant et des gaz), un ressort et un caillou à éjecter qui, par réaction, fera avancer la fusée (c’est le même principe que les gaz mais c’est plus évident à visualiser).
On aurait alors :
Ec_Fusée_initial + E_potentielle_ressort = Ec_Fusée_final + Ec_Caillou
Donc, avec 1/2 m_fusée = 1 :
Dans le cas 1 (fusée accélérant de v=0 à 10), on aurait donc :
0 + E_ressort = 100 + Ec_Caillou1
Donc : E_ressort – Ec_Caillou1 = 100
Dans le cas 2 (fusée accélérant de v=100 à 110) :
10000 + E_ressort = 12100 + Ec_Caillou2
Donc : E_ressort – Ec_Caillou2 = 2100
Je sais qu’en toute intégrité je devrais retrancher la masse du caillou pour le calcul de l’Ec finale de la fusée mais comme cette masse est très petite par rapport à la fusée et que cette masse n’évolue pas avec la vitesse (non relativiste) de départ, ça n’a pas grand intérêt. Mais si vous le souhaitez vous pouvez mettre 1/2 m_fusée_finale = 0,999999. En revanche, je prends bien sûr en compte Ec_Caillou 1 et 2 car les vitesses d’éjection peuvent être très grandes.
On sait que l’énergie potentielle de départ, E_ressort, est identique dans les deux cas. La relativité galiléenne (voir démonstration plus haut) le confirme.
La seule valeur pouvant nous faire retomber sur nos pattes est donc la différence entre Ec_Caillou1 et Ec_Caillou2.
Si ce n’est pas là que se situe la vérité, toute la physique classique s’effondre.
Heureusement, c’est bien là l’explication.
On a fait pour moi le calcul numérique (un chouia complexe, requérant l’utilisation de la formule de Tsiolkovski). Et le résultat est tombé : l’énergie potentielle du ressort (qui donc est constante dans les deux cas, dans tous les référentiels inertiels) est égale à… 10^8 + 300.
Et ce, avec les données numériques suivantes :
Masse fusée sans caillou = 0,999999
Masse caillou = 0,000001
J’ai même fait, pour vérifier, le calcul à rebours afin de m’assurer que les deux vitesses d’éjection du caillou (dans mon référentiel) avaient bien un différentiel de 100.
Et c’est le cas (v1=10 000 010 et v2=9 999 910) !
La loi de conservation de l’énergie mécanique et la relativité galiléenne sont sauvées !
En clair, si l’on considère un système dans son intégralité, un apport x d’énergie ne “rapporte” que x énergie et non x². Toutes les énergies en jeu doivent être comptabilisées pour que le paradoxe disparaisse.
Voilà !
Salut, bonsoir Christophe Delattre. Je tiens sincèrement à vous remercier pour ce bel exposé sur la formule E= mc2. Car j’ai pu trouvé quelques unes des réponses à mes questions concernant la célèbre formule d’Albert Einstein, car, n’étant pas du domain de la physique (je ne suis qu’un agronome, mais fan de la science astronomique, en particulier les travaux d’Albert Einstein), j’ai eu beaucoup du mal à comprendre concrètement ce que signifie réellement cette formule. Et grâce à votre article, j’ai pu trouvé satisfaction. Un grand merci en tout cas. Bonne continuité!
Un grand merci pour vos encouragements, et bonne lecture si vous avez d’autres articles à découvrir !
Remarquablement écrit. Sujet amené avec finesse. Explications…. explicite. Utilisation de formules pour démontrer tout ça (ça fait remonter des souvenirs d’études ca). Cet article est un bonheur à lire. Je vais m’empresser de lire les autres s’ils sont aussi bien écrit et complets. Merci vraiment. Les articles de cette qualité en français sont rares sur le Web. Je vais accompagné ce commentaire d’un petit don pour le travail effectué car il le mérite.
Un grand merci pour le don et pour les mots qui l’accompagnent ! J’ai souvent l’impression d’être de ces illuminés parlant tout seul dans une pièce fermée, et savoir que quelqu’un était là à m’écouter, ça me rassure. Vraiment. Encore merci !