Si vous n’avez pas lu les trois premières parties de ce formidable exposé, allez vous faire voir chez les Grecs, avant d’aller goûter au bûcher puis aux pommes et à l’éther luminifère…
Ah l’éther !…
Nous voilà donc en 1905. Depuis plusieurs années, la physique repose sur deux piliers : la Mécanique de Newton et l’Électromagnétisme de Maxwell. Deux cadres antagonistes, le premier formalisant la Relativité, le second imposant un référentiel absolu. Et puis il y a cette lumière et son étrange vitesse constamment constante quelle que soit notre propre vitesse par rapport à l’éther. Une révolution couve…
L’année miraculeuse
Il naît en 1879 dans le sud de l’Allemagne. Il confiera avoir été fasciné par une boussole à l’âge de cinq ans, et un livre de géométrie à treize ans. Il n’en sera pas de même avec le militarisme ambiant régnant dans l’Allemagne de cette fin du XIXe siècle. Contrairement à ses camarades, il exècre les défilés militaires. Souffrant de dyslexie et peu à l’aise avec l’autorité, son parcours scolaire s’en ressent. Malgré un très bon niveau en mathématiques, il sera finalement renvoyé de son lycée munichois à l’âge de 15 ans. La Bavière ne lui convient pas alors il se débrouille pour obtenir la nationalité suisse.
Après avoir échoué une première fois, il réussit son second examen d’entrée à l’École polytechnique de Zürich (nul besoin d’avoir le Bac ou son équivalent teuton). Il a 17 ans, et il y trouve son bonheur qu’il s’agisse de mathématiques, de physique, d’amitié (le mathématicien Marcel Grossmann que l’on retrouvera plus tard) ou d’amour (sa première épouse, Mileva).
Plus assidu en salle d’expérimentation qu’en cours, il obtient de justesse son diplôme en 1900. C’est ensuite une longue période de précarité, faute d’avoir pu obtenir un poste universitaire. Futur père et parce qu’il faut bien manger, il finit en 1902 par trouver un poste à l’Office des brevets de Berne en tant qu’expert de 3e classe (le bas du tableau). Pendant toutes ses années, il continue de cultiver sa curiosité pour la physique et la philosophie (et le violon) avec ses amis.
Et, en 1905, l’Univers bascule.

Si vous êtes arrivé jusque là, je pense que vous avez compris de qui il s’agit. C’est en effet le jeune Albert Einstein (26 ans) qui, entre le mois de mars et celui de septembre, va parvenir à publier cinq articles dans la revue scientifique allemande Annalen der Physik alors que, encore une fois, il n’est qu’un jeune et modeste employé de l’administration suisse, totalement inconnu du gotha scientifique. Ces cinq articles vont aborder des sujets très différents. Si l’un est intéressant, les quatre autres ont un caractère ré-vo-lu-tion-naire, méritant chacun plus qu’un Prix Nobel, et faisant de 1905 ce que l’on a nommé « l’année miraculeuse de la physique ».
La première de ces quatre révolutions, en mars, se nomme « Sur un point de vue heuristique concernant la production et la transformation de la lumière ». C’est cet article qui lui vaudra son seul Prix Nobel. Il s’agit ni plus ni moins de la véritable naissance de la Physique quantique ! Mais on contera une autre fois, l’histoire des grains de lumière et d’Albert au Pays des merveilles.
Le second de ces quatre articles, en mai, explique le mouvement brownien (l’agitation chaotique de microscopiques particules en suspension dans un liquide chaud), et fournit ni plus ni moins qu’une preuve théorique (vérifiée expérimentalement en 1912) de l’existence des atomes et des molécules !
Le troisième, en juin, s’intitule « Sur l’électrodynamique des corps en mouvement ». Quelques années plus tard, ces trente pages porteront le nom de « Théorie de la Relativité restreinte ». Et c’est cet article qui va ici nous intéresser.
Le titre du quatrième, en septembre, sera une question : « L’inertie d’un corps dépend-elle de son contenu en énergie ? » Et la réponse qu’il formule, entrera dans la postérité sous la forme : « E=mc² ». Nous allons aussi finir par en causer.
Le temps et l’espace ne sont pas ce que vous croyez
Vous avez suivi avec moi toute la controverse concernant cet éther luminifère, tout à la fois rigide, élastique et n’offrant aucune résistance à la matière, mais surtout détruisant toute idée de relativité en raison du référentiel absolu qu’il constitue. Il y avait aussi ces vagues d’éther (la lumière) semblant toujours se déplacer à la même vitesse quel que soit notre propre mouvement.
Einstein aborde son article de juin de manière radicale : puisque l’éther luminifère nous pose des problèmes, supprimons-le. Rassurez-vous, il sait ce qu’il fait. Le champ électromagnétique qui n’était alors que la représentation géométrique de la réalité, devient ici lui-même une réalité : une propriété de l’espace et du temps, la lumière (l’onde électromagnétique plus exactement) n’étant qu’une variation de cette propriété se propageant dans l’espace et le temps. Einstein est ainsi également à l’origine de ce que l’on allait nommer la théorie des champs.
On peut penser aussi que son premier article de mars, impliquant une dualité onde-corpuscule pour la lumière (comme je l’ai dit, on étudiera les photons une autre fois), l’a mis sur la voie. Mais s’il supprime l’éther luminifère, c’est surtout parce que cet éther s’oppose au principe de relativité. Et le principe de relativité, il trouve ça bien (et puis ce serait trop con que Bruno ait cramé pour rien). Surtout, en conservant ce principe, il a l’espoir de rendre enfin compatibles la Mécanique de Newton et l’Électromagnétisme de Maxwell.
Hormis le principe de relativité (je n’y reviens pas), il conserve le principe de causalité (la cause précède la conséquence) et ce fait expérimental qu’est la constance de la vitesse de la lumière (précisons « dans le vide » car cette vitesse décroît dans d’autres milieux comme l’air ou l’eau). Et il ne lui reste plus qu’à se demander à quoi l’univers peut bien ressembler si l’on ne tient pour vrai que ces trois choses-là, quitte à balancer le reste.
Cette constance de la vitesse de la lumière qui n’était alors qu’une illusion due à un vent d’éther dans nos atomes en mouvement, devient pour lui une réalité : quel que soit le référentiel dans lequel on se situe (le quai ou le train), la lumière aura toujours une vitesse égale à « c », même si sa source est en déplacement par rapport à vous. Et ce n’est plus une illusion, c’est réel !
Bien sûr, cela n’a aucun sens pour un physicien classique… comme pour vous, si vous avez suivi l’exemple de la lampe dans le wagon. Einstein répond que si cela vous semble contraire au bon sens, c’est que le temps et l’espace ne sont pas ce que vous croyez.

Là, c’est important de bien comprendre.
Il est des choses qui nous paraissent évidentes, bêtes comme choux. Un bâton d’un mètre fait un mètre de long, que vous l’aperceviez sur votre quai ou dans le train passant devant vous. Une minute dure une minute à l’horloge du quai ou sur la montre d’un passager de ce train. Le temps – et je parle bien de celui de votre montre – s’écoule inexorablement, de la même manière, dans tous l’univers. De même, un quai à une longueur identique que vous soyez sur ce quai ou dans le train ou sur la Lune. Il n’y a pas des « temps » différents ou des « mètres » différents selon la vitesse de ceci ou de cela. De même, deux évènements simultanés sont simultanés, point. En physique classique, c’est ce que l’on appelle des absolus. C’est pour nous une évidence, et tout ça n’a pas grand intérêt.
Pour Einstein, vous avez tout faux, et c’est là la clef du problème.
Si l’on conserve le principe de relativité, le principe de causalité et la constance de « c », on en déduit – avec Einstein – des choses qui vous paraîtront absurdes, et dont Albert fait le pari qu’elles sont on-ne-peut-plus réelles.
Et je peux déjà vous confier que ce pari a été gagné. Il est en fait gagné chaque jour, dans votre smartphone muni d’un GPS.
Décrivons ces choses à l’aide d’un quai sur lequel vous vous dorez la pilule, d’horloges, de quelques longueurs, de lampes, d’un miroir et d’un train passant devant vous, un train ultra rapide (genre faisant plusieurs tours de la Terre en une seconde)…
Relativité du temps
Présentation
La première conséquence de cette théorie est que le temps n’est plus absolu : le temps se dilate dans un référentiel se déplaçant par rapport à vous.
En termes simples, si vous observez la montre d’un passager du train, vous verrez ces aiguilles tourner moins vite que celles de votre propre montre : son temps n’est pas le vôtre. Surprenant non ?
Mais il y a mieux : l’expérience est identique pour le passager. S’il observe votre montre, il verra, cette fois-ci, vos aiguilles tourner moins vite que sur sa montre !
C’est l’essence même du principe de relativité : pour lui, il est comme immobile, et c’est votre quai qui se déplace en sens inverse. Les deux situations sont totalement symétriques, et doivent, de ce fait, aboutir aux mêmes conclusions, même si elles paraissent contradictoires.
Lequel de vous deux a raison ? Les deux, bien sûr. Le temps n’est plus un absolu, et il dépend de votre point de vue. Le temps devient relatif (il dépend du référentiel considéré).

Explication
Pas d’équation, promis. Mais il va falloir quand même se concentrer un peu.
Imaginons que le voyageur place un miroir sur la vitre du train, puis une lampe avec détecteur de lumière, côté couloir. Si L est la distance entre la lampe et le miroir, la lumière parcourra donc « 2 L » (aller + retour). Laissons le mesurer le temps que mettra la lumière pour aller vers le miroir puis en revenir. Disons, par exemple, qu’il obtient « 2 » sur son chronomètre (en secondes ou en milliardièmes de seconde, peu importe pour notre démonstration). C’est le joli schéma que j’ai pondu ci-dessous…
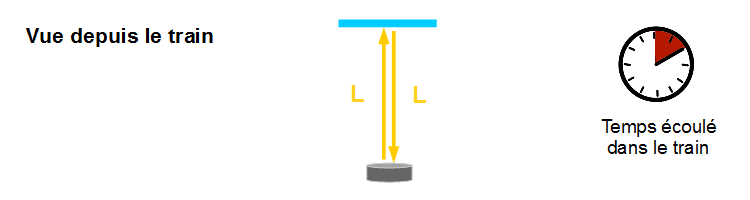
Maintenant, observez cette expérience depuis votre quai. Pour vous, entre le moment où la lumière sort de la lampe et le moment où elle atteint le miroir, le train s’est déplacé. De votre point de vue, la lumière aura donc dû parcourir un trajet plus long que L, et que nous nommerons L’. Même chose entre le miroir et le retour à la lampe. Schéma encore plus joli ci-dessous...
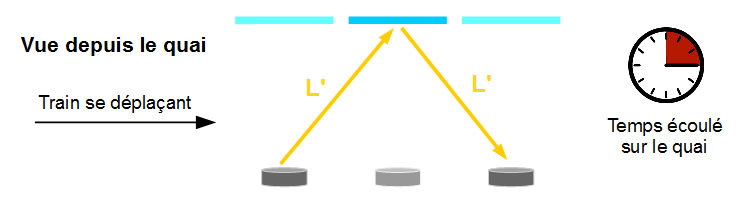
En physique classique, cela ne pose aucun souci : le rallongement du trajet est parfaitement compensé par l’augmentation de la vitesse de « l’objet » en question (ici la lumière) puisque cet « objet » est situé dans un train qui, lui-même, se déplace.
Mais… ici, ce n’est pas possible : on a pris pour principe que la vitesse de la lumière sortant de la lampe sera constante, qu’elle soit mesurée dans le train ou depuis le quai. Et donc, la lumière allant à la même vitesse mais parcourant un trajet plus long « 2 L’ », elle mettra, pour vous, plus de temps pour revenir à la lampe. « Plus de temps » signifie que votre chronomètre sur le quai affichera, par exemple, « 3 » à la fin de l’expérience (le nombre dépendant de l’allongement du trajet, c’est à dire de la vitesse du train).
Donc résumons le résultat de cette expérience. Entre le départ de la lumière et son retour à la lampe, vous avez mesuré un temps égal à « 3 », alors que le chronomètre présent dans le train s’est, lui, arrêté sur le chiffre « 2 ». Une seule conclusion : le chronomètre présent dans le train va moins vite que le vôtre. Ces aiguilles tournent moins vite. Ou, plus exactement, le temps du train n’est pas le temps du quai : il vous semble dilaté par rapport à votre temps… Bienvenue au Pays d’Albert.
Et n’oubliez pas que, pour le voyageur (relativité oblige), les conclusions sont inversées : c’est votre temps qui lui semble dilaté. Lorsqu’il a arrêté son chronomètre à « 2 », de son point de vue, le vôtre était encore à « 1,3 ». Eh oui, alors que l’expérience venait de se terminer, elle était, selon lui, encore en cours pour vous. Et là, le peu de bon sens qu’il vous reste, part en quenouille.
Ok, il semble y avoir également quelque chose d’étrange qui se passe au niveau de la simultanéité des évènements. Voyons cela de plus près…
Relativité de la simultanéité
Présentation
Ici, la notion de simultanéité absolue n’existe plus : deux événements qui semblent simultanés dans un référentiel, ne le sont pas dans un autre référentiel.
En termes simples, si pour un passager du train, son voisin éternue au moment même où le contrôleur ouvre la porte (deux événements simultanés), vous, sur votre quai, vous verrez cette personne éternuer alors que le contrôleur est encore dans le wagon d’à côté.
De même, deux événements (survenant sur le quai, dans le train ou sur la Lune) qui vous paraîtront simultanés sur votre quai, ne le seront pas pour le voyageur.
Comprenez bien : il n’existe plus d’événements simultanés au sens où vous l’entendez. La simultanéité absolue suit le même chemin que le temps absolu. La simultanéité devient relative (elle dépend du référentiel dans lequel on se place).
Explication
Allez, on se re-concentre…
On reprend notre train ultra-rapide. Re-précisons que pour un voyageur s’y trouvant, le train est immobile, c’est le paysage qui défile ultra-rapidement.
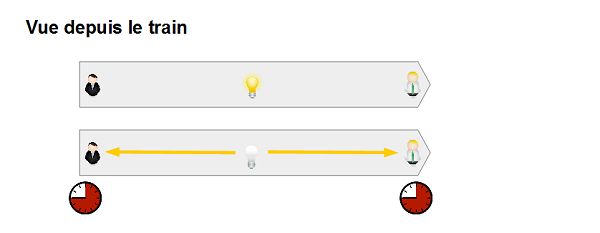
Au milieu de ce train, on place une ampoule qui déclenchera un flash lumineux quand notre voyageur appuiera sur le bouton. Un monsieur blond en chemise se place à la tête du train pendant qu’un monsieur brun en veste se place, lui, à la queue du train. Tous deux disposent d’un chronomètre qu’ils stopperont lorsqu’ils verront le flash, c’est à dire lorsque la lumière partie de l’ampoule les atteindra. Comme cette ampoule est placée exactement au milieu du train, la lumière parcourra la même distance d’un côté comme de l’autre.
Faisons l’expérience (schéma ci-dessous)… Sans surprise, les deux obtiennent le même résultat sur leur chronomètre. On va dire que l’aiguille se situe sur « 9 ». Vous êtes donc d’accord pour dire que les deux évènements (« la lumière arrive en queue de train » et « la lumière arrive en tête de train ») sont simultanés. Jusque là, rien de plus normal.
Observons maintenant cela depuis notre quai…
Si le voyageur avait shooté dans un ballon, nous n’aurions pas mesuré une même vitesse selon que ce ballon ait été envoyé vers l’avant ou vers l’arrière du train. Mais là, il s’agit de lumière. Et nous avons pris pour principe que la vitesse de la lumière que nous mesurerons depuis notre quai sera identique, qu’elle parte vers l’avant ou vers l’arrière. Et donc, voilà ce qui se passe, de notre point de vue…
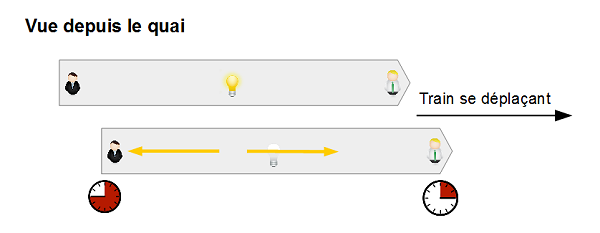
Lorsque le flash est émis, messieurs Blond et Brun se situent à égale distance de l’ampoule. Mais, pendant que la lumière avance vers eux, le train se déplace vers la droite. De ce fait – et de notre point de vue – la lumière va atteindre M. Brun, situé à l’arrière, bien avant qu’elle n’atteigne M. Blond (schéma ci-dessus).
On sait que le chronomètre de M. Brun affiche « 9 » lorsqu’il reçoit la lumière. Ce sera la même chose pour M. Blond lorsqu’il aura reçu le flash. Mais là, c’est loin d’être le cas. Le chronomètre de M. Blond doit afficher quelque chose comme « 3 » (vous l’avez compris, ce nombre dépend de la vitesse du train par rapport à nous). Lorsque M. Blond recevra enfin la lumière, M. Brun sera peut-être déjà parti boire un café.
Il s’agit de la même scène. Et pourtant, ici, les deux événements dont nous parlions ne sont plus du tout simultanés. Et bien sûr si deux autres événements nous paraissaient simultanés depuis notre quai, ils ne le seraient pas pour le voyageur du train. Dire que deux événements sont simultanés n’a donc pas vraiment de sens. Sauf si l’on précise dans quel référentiel on se situe. La simultanéité est donc… relative.
Relativité des longueurs
Présentation
On n’a pas fini de jouer avec vos sens. Pour l’instant, nous avons parlé du temps. Parlons à présent de l’espace. De longueurs, si vous préférez. Cette théorie de la Relativité implique en effet que quelque chose se déplaçant par rapport à vous, vous apparaîtra contracté dans le sens de ce déplacement.
Oui, je sais, dans les précédents schémas, j’aurai dû faire les trains plus courts quand ils étaient vus depuis le quai. Mais cela vous aurez troublé inutilement, et surtout cela n’aurait rien changé au raisonnement tenu (vous pouvez vérifier).
En clair, si vous mesurez un train à l’arrêt et que, par exemple, il fasse la même longueur que votre quai, exactement entre deux poteaux, et que, le lendemain, vous le preniez en photo (temps de pose quasi nul bien sûr) alors qu’il passe à vitesse ultra-rapide devant ce quai, vous obtiendrez un surprenant cliché. Le train y apparaîtra plus court, bien à l’intérieur de vos deux poteaux.
De même si, au moment de cette traversée, messieurs Brun et Blond (de l’exemple précédent) situés à chaque extrémité du train, prennent eux aussi une photo, il y a de fortes chances pour que M. Brun obtienne un cliché de la campagne (le train n’est pas encore arrivé au quai), et que M. Blond obtienne un cliché de la ville (le train a déjà dépassé le quai). Pour eux, le quai est donc plus petit que le train. Pour eux, c’est le quai qui se déplace… et qui s’est donc contracté.
Explication
Quant à vous, il faut vous décontracter… puis vous concentrer à nouveau.
Pour mieux comprendre nous allons prendre deux trains (un bleu et un blanc) se croisant à la même vitesse devant votre quai. Il y a quelques jours, nous les avions mesurés en gare, et ils avaient la même longueur. Cette fois-ci, ils nous apparaissent plus courts mais vous n’êtes pas encore obligé de me croire. Notons que, Albert ou pas, raccourcis ou pas, comme ces trains vont à la même vitesse (même si c’est en sens opposés), ils nous apparaissent, l’un et l’autre, de longueur identique.
Oublions notre quai, pour l’instant, et concentrons-nous sur le train blanc. La longueur de ce train n’a pas changé pour les passagers situés à l’intérieur. Pour eux, c’est comme s’il était immobile. Nous allons plutôt leur demander de mesurer la longueur du train bleu passant devant eux. Pour cela, il existe un moyen tout simple : les passagers se placent à chaque fenêtre du train blanc. On sait à peu près que le train bleu passera quand l’aiguille de leur montre sera sur « 6 » (aiguille pointée vers le bas). Nous allons donc leur demander de regarder leur montre et, lorsque l’aiguille sera sur « 6 », de regarder par la fenêtre puis de nous dire ce qu’ils ont vu.
Et vous allez être surpris (schéma ci-dessous). C a vu « du train ». E et A ont vu « le paysage ». D a vu la tête du train, et B, la queue du train. Pour les passagers du train blanc, le train bleu a une longueur D-B, inférieure à celle de leur train blanc.
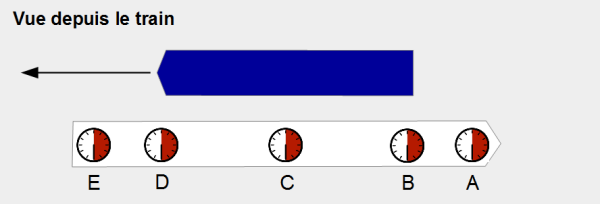
Pour mieux comprendre, observons nous aussi cette scène depuis notre quai (schéma ci-dessous). Notons que les montres des passagers nous semblent ici totalement désynchronisées (c’est la relativité de la simultanéité vue précédemment).
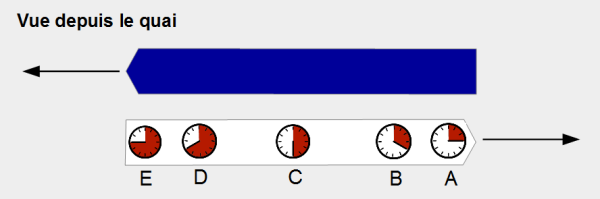
On peut, dès lors, facilement comprendre pourquoi les passagers ont vu ce qu’ils ont vu lorsque l’aiguille est arrivée sur « 6 ».
Le passager C a vu « du train » (c’est clairement indiqué sur le schéma).
Pour A, en revanche, l’aiguille n’est pas encore sur « 6 ». Quand elle y arrivera, la queue du train ne sera plus devant lui. A « 6 », il a donc vu « du paysage ».
Pour E, l’aiguille est déjà sur « 9 ». Quand elle était sur « 6 », la tête du train n’était pas encore arrivée devant lui. Il a donc vu « du paysage ».
Même principe pour B et D qui au temps « 6 », du fait du décalage de leur montre, ont dû respectivement voir la queue et la tête du train bleu.
Pour les mêmes raisons, les passagers du train bleu penseront que c’est le train blanc qui est plus court que le leur (nous aurions le même schéma mais avec l’ordre des voyageurs et leur montre inversés puisque leur train va dans l’autre sens).
Et c’est ce même principe qui, sur le quai, nous fera voir ces deux trains plus courts que la mesure faite à l’arrêt en gare. Bien sûr la contraction de la longueur dépend de la vitesse de l’objet par rapport à l’observateur. Et le train bleu va plus vite pour les passagers du train blanc que pour, nous, qui sommes sur le quai. Ils verront ce train bleu encore plus contracté que nous.
Pour résumer, le train bleu a une longueur L pour ses passagers. Pour nous, il a une longueur plus courte que L. Pour les passagers du train blanc, il a une longueur encore plus courte que L.
Qui a raison ? Tout le monde. Quelle est la longueur du train bleu ? Elle n’existe pas de façon absolue. Elle dépend du référentiel dans lequel on la mesure. La longueur est, elle aussi, relative !
« c » est un mur
Présentation
« c » est une vitesse. C’est la vitesse de la lumière dans le vide mais, plus généralement, la vitesse dans le vide de toute particule sans masse. La lumière – qui n’a pas de masse – n’en est juste que l’exemple le plus connu, l’exemple qui nous aura permis de découvrir tout ceci. Et quand on dit qu’il s’agit de la vitesse de ces particules, il s’agit bien d’une vitesse absolue (on obtiendra la même mesure quel que soit notre référentiel). Je n’y reviens pas, c’est ce qui nous vaut tous les phénomènes étranges, toutes ces dilatations et contractions que l’on vient d’observer.
Mais nous n’en avons pas fini avec les choses qui heurtent l’esprit, qui heurtent votre bon sens.
Il découle en effet de la relativité d’Einstein qu’aucune particule ayant une masse, ne peut atteindre cette vitesse c, et encore moins la dépasser. Et quand je parle de particules massives, je parle de celles qui vous composent, qui composent la matière. Je viens donc de vous affirmer qu’aucun train, aucune fusée, aucun gamin avec un ballon, aucun ballon shooté par un gamin, ne pourra atteindre la vitesse c. Et ce n’est pas parce qu’on n’a pas encore inventé le moteur du Faucon Millenium de la Guerre des étoiles. Non, le problème n’est pas technique… c’est tout simplement physiquement impossible.
Là, vous vous dites… Il est gentil le gars. Mais, si j’observe une fusée allant presque à la vitesse de la lumière, et qu’à l’intérieur, un gamin shoote dans le ballon vers l’avant. Le ballon, lui, il dépassera la vitesse de la lumière.
Bah non.

Explication
Le facteur servant à calculer les dilatations du temps et contractions de l’espace, a parfaitement été décrit par Lorentz et Poincaré. Il dépend lui-même de la vitesse de l’objet observé. Je vous en parlerai un peu mieux par la suite. Sachez toutefois qu’il ne représente quasiment rien pour les vitesses usuelles mais augmente de manière drastique à mesure que l’objet s’approche de la vitesse de la lumière.
Concrètement, la fusée en question nous apparaîtra toute aplatie, et la distance parcourue par le ballon, réduite à presque rien. En outre, l’aiguille d’une horloge placée dans la fusée, nous semblera presque immobile, l’action du shoot se déroulant dans un ralenti extrême. Bref, la vitesse supplémentaire du ballon que nous calculerons, sera si faible qu’elle n’atteindra jamais c. Et même si l’on cherche à se rapprocher encore plus de c au niveau de la fusée, les effets sur la vitesse relative du ballon (celle que l’on observe depuis la Terre) seront encore plus importants, faisant que ce ballon n’atteindra jamais la vitesse de la lumière. Jamais.
Et c’est la même chose pour la fusée elle-même. Si le pilote décide de donner un énorme coup de booster, vue de la Terre, l’augmentation de la vitesse nous paraîtra infime, et d’autant plus infime que la vitesse de la fusée semble s’approcher de c. Et le pilote s’apercevra aussi que le Terre ne s’éloigne pas autant qu’il l’aurait espéré. Lui, non plus ne verra jamais cette Terre toute plate, toute ralentie, s’éloigner de lui à la vitesse de la lumière.
Mais bon, on peut s’amuser en se demandant à quoi ressemblerait, pour nous, depuis la Terre, une fusée allant à la vitesse de la lumière (ce qui – rappelons-le – est impossible). La fusée aurait tout simplement une longueur nulle, et le temps y serait à l’arrêt.
Causalité
Donc, pour tout ce qui a de la masse, la vitesse mesurée ne peut être qu’inférieure à c. Pour ce qui n’a pas de masse, toute vitesse mesurée est égale à c. Notons au passage qu’aucune information ne peut donc être transmise plus vite que c.
Et tout cela nous arrange bien (et peut-être l’univers aussi) car nous avons conservé un autre principe que la relativité : le principe de causalité. Vous vous souvenez de notre exemple avec M. Brun et M. Blond concernant la non-simultanéité : deux événements simultanés dans le train, ne l’étaient plus, vus depuis le quai. Dans cet exemple, il y avait également un troisième événement : le déclenchement du flash par le passager au centre du train. Appelons-le « événement flash », et les deux autres, événements « brun » et « blond ». Cet événement flash est particulier par rapport aux deux autres puisqu’il en est la cause. Et les deux autres en sont les conséquences. Sans flash, pas de lumière parvenant à Blond et Brun.
Par rapport à notre quai, plus le train se rapprochera de la vitesse de la lumière, plus les événements blond et brun nous paraîtront se désynchroniser. Si le train allait à la vitesse de la lumière (ce qui est impossible), nous constaterions des choses aberrantes. L’événement blond n’arriverait jamais alors même que M. Blond se situe au même endroit que la lampe, de tout ce qu’il y a dans le train, et du train lui-même (puisque celui-ci, comme tout le reste, a une longueur nulle). Quant à l’événement brun, il intervient au même instant que l’événement flash dont il est la conséquence (ce qui est déjà très limite quant à la causalité).
Poussons le bouchon encore plus loin, et imaginons que le train aille plus vite que la lumière. Et là, on viole brutalement le principe de causalité : l’événement brun se produit avant l’événement flash. Oui, ici, la conséquence précède la cause… C’est comme si notre voyageur buvait sa canette avant d’avoir été la récupérer dans son sac.
Inutile de prendre un cachet d’aspirine car, comme nous l’avons montré avec la fusée, les Lois de la relativité empêchent le train d’atteindre ou de dépasser « c ». Comme vous, l’univers peut souffler, et c’est là une nouvelle raison de considérer « c » comme un mur infranchissable.

Un petit mot sur les tachyons pour terminer. Un « tachyon » est un type de particules hypothétiques résultant de théories physiques nées dans les années 60. La particularité d’un tachyon, c’est qu’il va obligatoirement plus vite que la lumière. Pour respecter les Lois de la relativité, il possède des propriétés pour le moins étranges. Ainsi, son énergie diminue à mesure que sa vitesse augmente. Et le nombre qualifiant sa masse est, au sens mathématique, un imaginaire pur (un nombre dont le carré est négatif).
Ne vous enflammez pas : bien qu’étant d’un réel intérêt scientifique, ces particules demeurent très hypothétiques, tout comme les théories en question.
Le paradoxe des jumeaux de Langevin
Jusqu’ici, tout ce que nous avons dit ressemble à des effets de perspective : votre train est plus court que le mien, et pour vous, c’est l’inverse. C’est un peu comme lorsque je vous regarde de loin : vous semblez très petit par rapport à moi, et de votre côté, c’est l’inverse… mais nous savons très bien que nous mesurons à peu près la même taille. Si vous venez rapidement me rejoindre, vous n’allez pas conserver une taille de 3cm. Tous les effets que nous venons de décrire seraient donc une simple illusion ? En fait, non. Et nous allons le comprendre.
Ce sujet a été abordé par le physicien français, Paul Langevin, lors d’un congrès en 1911. D’où son nom : le paradoxe des jumeaux de Langevin. Toutefois, sachez qu’il avait été examiné auparavant, notamment par Einstein. Sachez également que Langevin n’y parlait pas de jumeaux, ni même de paradoxe. Ceci étant dit, voyons de quoi il s’agit, et décrivons cela de la manière la plus communément utilisée aujourd’hui. Mais je vais quand même y mettre ma touche personnelle…
Nous avons donc deux frères jumeaux, Casanier et Baroudeur (si vous cherchez un prénom pour votre enfant, demandez-moi). Ceux-ci mettent au point une fusée à propulsion unobtainiumique (ne cherchez pas sur Wikipedia) permettant de voyager à une vitesse très très très rapide, une vitesse proche de c.

Casanier décide de rester sur Terre pendant que son frère, Baroudeur, grimpe dans la fusée et s’en va pour un voyage d’un an vers les étoiles. Vers les étoiles ? Oui car les distances « astronomiques » nous séparant des étoiles, et que nous avions calculées sur Terre, se retrouvent contractées, vues depuis la fusée. Après six mois, Baroudeur décide de faire demi-tour, et encore six mois plus tard le voilà de retour sur Terre.
Baroudeur débarque sur l’astroport mais avant de s’adresser à la foule en liesse, son premier geste est pour son frère : il va fleurir la tombe de Casanier, mort de vieillesse, cinquante ans auparavant.
Ouaip.
Surprenant, non ?… Mais le paradoxe n’est peut-être pas là où vous le croyez. Souvenez-vous notamment que les effets dont nous parlions étaient parfaitement symétriques d’un référentiel à l’autre. Si l’horloge de la fusée tourne moins vite selon Casanier et ses amis terriens, l’impression est la même pour Baroudeur vis-à-vis des horloges terrestres. Baroudeur aurait donc pu s’attendre à ce que son frère Casanier n’ait vieilli que de quelques jours pendant que, lui, passait un an dans sa fusée. Et pourtant… fleurs… tombe. Voilà le vrai paradoxe.
Autant vous le dire tout de suite, cet apparent paradoxe n’en est pas un. Tout vient de cette erreur : considérer que Casanier et Baroudeur ont vécu des situations symétriques. Ce n’est pas le cas. Contrairement à Casanier, Baroudeur et sa fusée ont subi une accélération pour passer du référentiel « Terre » au référentiel « Dudju qu’ça va vite ». La fusée a dû ensuite ralentir pour faire demi-tour, puis ré-accélérer pour revenir avant de freiner à nouveau pour se poser. Alors que Casanier demeurait dans son référentiel (la Terre), Baroudeur n’a pas arrêté d’en changer. Tout vient de là.
Ce coup-ci, je ne vais pas tenter de vous le prouver. Pour plusieurs raisons : je fatigue, c’est un peu complexe pour moi, ça l’est assurément trop par rapport à ce que je veux vous proposer sur ce site, et enfin il y a débat pour savoir si ce qu’il y a ici suffit à expliquer le phénomène ou s’il faut avoir recours à ce que je vous raconterai prochainement. Mais l’expérience le montre, c’est bien ainsi que ça se passe, comme nous allons le voir…
Mise à l’épreuve
En 1905, en pleine expansion du trafic ferroviaire, il devenait urgent de trouver un moyen de synchroniser les horloges des gares d’un même pays. Le fait qu’Albert Einstein, pour son travail d’analyse à l’Office des brevets, ait reçu de nombreux projets de synchronisation des horloges, n’est peut-être pas sans rapport avec ses réflexions sur le sujet, réflexions qui allaient aboutir à cet article de juin.
Toutefois, rassurez-vous pour vos correspondances entre Paris et Marseille, la vitesse des trains (TGV y compris) est bien trop faible pour que les effets décrits ci-dessus soient à prendre en compte. Dans notre vie quotidienne, la physique de Galilée et Newton suffit amplement. Voyons pourquoi…
Ca fait combien « c » ?
« c » est une vitesse égale à 299 792,458 km/s, soit à peu près trois cent mille kilomètres par seconde. Vous avez du mal à vous rendre compte de ce que cela peut représenter ? Ok, vous allez faire claquer vos doigts (ou vos mains), attendre à peine plus d’une seconde puis claquer une seconde fois.
Faites-le… Oui, pour de vrai.
Entre ces deux claquements, la lumière a fait huit fois le tour de la Terre !
Ca va ? Vous vous rendez un peu mieux compte de ce que représente cette vitesse ?
A côté de cela, les vitesses « v » des objets qui nous entourent (voitures, trains, avions, fusées, short d’Usain Bolt) sont « microscopiques ». L’engin le plus rapide construit par l’homme (sonde solaire Helios 2) a une vitesse de 70 km/s.
Un (tout petit) peu de maths
Je vous l’avais promis, le voici… Le facteur qui entre en jeu dans les transformations de Lorentz, celui qui permet de calculer les contractions d’espace et dilatations du temps que nous avons décrites, est le suivant :
S’il vous reste quelques bribes de bases de mathématiques du collège, vous pouvez en déduire ceci :
- Si v (la vitesse du train ou de quoi que ce soit) est très petite par rapport à c, la division de leurs carrés va tendre vers 0, et l’ensemble tendre vers 1. Et un facteur égal à 1, ça n’a aucun effet. Voilà pourquoi notre quotidien ne ressemble pas à tous ces phénomènes étranges précédemment décrits, pourquoi notre bon sens est ce qu’il est, et pourquoi on continue d’utiliser la mécanique de Newton, apprise au collège.
- En revanche, si v se rapproche de c, alors la division de leurs carrés va tendre vers 1, ce qui est en-dessous de la barre va tendre vers zéro, et l’ensemble va tendre vers l’infini. Et l’infini, c’est grand (si j’ose dire). Là, on est en plein dans les phénomènes étranges que nous avons décrits. C’est pourquoi on ne peut atteindre c (les contractions et dilatations deviennent infinies).
- On peut enfin noter que si v était supérieur à c, ce qu’il y a à l’intérieur de la racine carrée deviendrait négatif. Ce qui ferait saigner du nez vos anciens profs de collège.
Ce facteur n’est pas arrivé là par hasard. Il est la conséquence directe de la constance de c. Pour ceux qui auront envie, je mettrai ci-dessous une vidéo expliquant comment le retrouver mathématiquement.
Vérification et usage
Pas de suspense inutile, la théorie a bien été vérifiée. Ce qui ne veut pas dire qu’elle ne sera pas, un jour, à son tour, prise à défaut, nous obligeant à construire un nouveau modèle. On a même cru que cela était arrivé en 2011 avec une expérience nommée Opéra qui semblait montrer que des neutrinos (particules très faiblement massives mais massives quand même) s’étaient déplacés plus rapidement que c. L’excitation des physiciens est vite retombée : l’erreur était due à un câble mal branché.
L’exemple le plus couramment donné pour illustrer les effets relativistes, concerne les muons. Ce sont des particules qui ont une durée de vie de 2,2 microsecondes (après, ils se transforment en d’autres choses). Des muons sont constamment créés par le rayonnement cosmique dans la haute atmosphère terrestre. Leur durée de vie ne leur laisse a priori pas assez de temps pour atteindre le sol. Or nos capteurs au sol les captent. Vous avez compris : « l’horloge » de ces muons ultra-rapides est, pour nous, si ralentie qu’ils nous arrivent en étant encore dans leur prime jeunesse. Et le trajet effectué qui nous paraît si long, est en fait très court pour un muon.
Même si d’autres effets entrent en jeu, j’aurais pu également vous parler des expériences faites avec des horloges atomiques ultra-précises, l’une restant au sol, l’autre étant embarquée dans un jet. Et à l’atterrissage, on peut effectivement constater la désynchronisation de ces deux horloges (c’est l’exemple des jumeaux de Langevin). Et l’écart, ici infime mais réel, est conforme à la théorie.
Bon, soyons clairs, ces lois relativistes ont été testées et continuent de l’être avec des dispositifs de plus en plus perfectionnés, avec une précision de plus en plus fine. Et les résultats sont toujours en parfait accord avec la théorie.

Comme indiqués précédemment, ces lois relativistes ne sont réellement utiles que dans deux cas :
- Lorsque la vitesse de l’objet étudié est ultra-rapide : c’est par exemple le cas des particules utilisées dans les accélérateurs tel le LHC à Genève (ci-dessus).
- Lorsque nous avons besoin d’une précision ultra-fine : c’est par exemple le cas des satellites GPS (sachant que d’autres effets entrent aussi en jeu).
Mais bon, pensez à remercier Albert lorsque vous arriverez à bon port, en voiture, sur votre lieu de vacances.
…
Whaouuu… Là, je viens de battre mon record de longueur de page. Merci d’être parvenu jusque là !
Et nous ne sommes qu’en juin 1905. L’année miraculeuse d’Einstein n’est pas terminée : il lui reste un article à écrire. Il l’enverra en septembre.
Cela vous intéresse de savoir de quoi il cause ? Alors, allons découvrir les secrets de… « E=mc² » !
Bonus vidéos
Comme promis…
Cours de relativité restreinte
Un cours très accessible d’initiation à la relativité restreinte (par Richard Taillet), et vous y retrouverez certains exemples de cette page…
Parenthèse Culture
Si vous souhaitez passer une heure très intelligente en compagnie d’Etienne Klein, c’est ici…
La relativité restreinte expliquée en animation
Si vous voulez d’autres exemples avec des trains, des fusées et des horloges (par Alain Bernard)…
La relativité
- Partie 1 : ce n’est pas absolu
- Partie 2 : c’est l’égalité
- Partie 3 : ça se contracte
- Partie 4 : c’est révolutionnaire
- Partie 5 : c’est aussi « E= mc² »
- Partie 6 : c’est général
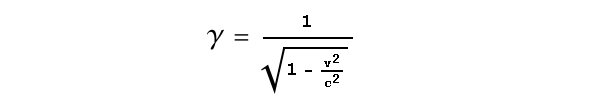





Dans la plupart des textes sur la relativité restreinte le statut de la dilatation des durées et de la contraction des longueurs n’est pas clair. S’agit-il d’un phénomène de perspective (comme la longueur apparente des objets éloignés) qu’il faut interpréter par les transformations de Lorentz ou bien s’agit-il de phénomènes qui existent vraiment comme proposé par le paradoxe des jumeaux ?
Merci pour la réponse.
A priori, le paradoxe des jumeaux ne s’inscrit pas dans le cadre de la relativité restreinte du fait des accélérations. Il est, en revanche, parfaitement expliqué dans le cadre de la relativité générale. Maintenant, j’avoue avoir lu que cela pouvait être expliqué par la seule RR mais je n’ai jamais vu d’explication cohérente à ce sujet.
Ah! cher ami, comment vous remercier (vous et vos semblables) pour cette somme de travail qui nous rend accessible des théories si contre-intuitives?
J’attends la suite avec impatience.
Bien à vous
Votre mot est en soi un grand remerciement… et me permet surtout de croire qu’au moins une autre personne que moi lit ma prose. Et ça fait chaud au cœur. Quant à la suite, je devrais pouvoir dégager du temps avant la fin du mois de décembre. A bientôt, donc.