Si vous avez bien suivi toute cette histoire, avec les Grecs, les inquisiteurs, les barbus, le moustachu ébouriffé et sa célèbre équation, le concept de relativité ne devrait plus avoir de grand secret pour vous. Depuis le début, la physique s’est bâtie, s’est transformée, nous a bouleversés afin de respecter ce principe de relativité : les lois de l’univers s’expriment de la même manière pour tous les référentiels inertiels.
Nous ne sommes pourtant pas parvenus au bout du chemin car, comme l’écrivait Albert Einstein : « Il est absolument possible qu’au-delà de ce que perçoivent nos sens, se cachent des mondes insoupçonnés. »

Ce qui va suivre aurait pu être découpé en plusieurs articles mais, pour conserver une certaine unité, et vu que nous en sommes déjà à la sixième partie de cet exposé, tout a été réuni ici, tel un bouquet final. Cela va donc être un peu long. Mais je vous promets à nouveau qu’il n’y aura aucune équation (ou alors, juste pour faire joli), et que j’essaierai de ne pas être rébarbatif. J’essaierai… Allez, venez franchir la ligne d’arrivée avec moi (et Albert), ça vaut le coup.
Mais… pourquoi Relativité « générale » ?
Une petite piqûre de rappel s’impose…
Enfermé dans votre laboratoire insonorisé et clos, il vous est impossible de savoir si celui-ci est posé au milieu d’un pré ou sur un train roulant à vitesse constante. Ou autrement dit, si vous mangez un hamburger dans votre salon, le ketchup tombera sur votre cuisse. Si vous le mangez dans votre voiture, sur l’autoroute, à vitesse constante, le ketchup n’ira pas tâcher le pare-brise ou la vitre arrière, il tombera aussi sur votre cuisse. Cela vous permet de dire que c’est votre voiture qui est immobile et que c’est la Terre qui défile sous vos roues à vitesse constante… ou l’inverse. Peu importe, quel que soit le référentiel inertiel que vous choisissez (voiture ou Terre), les lois physiques demeurent les mêmes. Il n’y a pas de référentiel absolu, c’est le concept de relativité. Cela a l’air tout con mais, pour le conserver, cela a quand même abouti, en 1905, à E=mc² et à une refondation des concepts d’espace et de temps.
L’histoire du ketchup sur votre cuisse, c’est ce que l’on appelle un « principe d’équivalence » : manger dans ma voiture équivaut à manger dans mon salon, les lois de la nature sont les mêmes. Ceci étant dit, évitez quand même de manger dans votre voiture car si, en essuyant le ketchup, vous percutez un arbre, alors votre voiture, durant un bref instant, ne sera plus un référentiel inertiel (car décélération brutale). Après ce bref instant, votre voiture redeviendra un référentiel inertiel (tout comme l’arbre), alors que vous, vous ne serez plus grand chose après avoir été répandu comme du ketchup sur ce qui était le pare-brise.
Et c’est là que ça titille. Ce principe d’équivalence ne vaut que pour les référentiels inertiels, ceux qui ne subissent aucune accélération (ou décélération, ou rotation, ce qui équivaut à des accélérations d’un point de vue physique). Et c’est ici qu’intervient à nouveau notre Zorro de la Physique. Albert Einstein va en effet énoncer un nouveau principe d’équivalence, et ce qu’il va en déduire, va vraiment éblouir le Monde. Et comme, cette fois-ci, cela va concerner la totalité des référentiels, inertiels ou pas, tout ce qui va suivre dans cet article, sera nommé « Relativité générale », et ce qui a précédé, en 1905, deviendra la « Relativité restreinte ».
Un petit gros bémol toutefois. Beaucoup préférerait inverser les deux qualificatifs car, en 1905, ce sont les fondamentaux de la physique – l’espace, le temps, la masse, l’énergie – qui avaient été métamorphosés. Ici, il s’agit d’une théorie qui ne va remettre en cause que l’une des deux forces connues à l’époque : la gravitation. D’ailleurs la traduction puis les années ont un peu joué leur rôle, les noms allemands originaux étant « théorie particulière de la relativité » et « théorie généralisée de la relativité ».
Toutefois, ne vous méprenez pas sur l’importance de la chose : avec la Relativité générale, il s’agit bien d’un cataclysme qui va modifier pour toujours notre vision de l’univers.
La pomme de Newton
Depuis le XVIIème siècle, la Loi de l’attraction universelle (la gravitation) était, à juste titre, devenu un monument de la science.
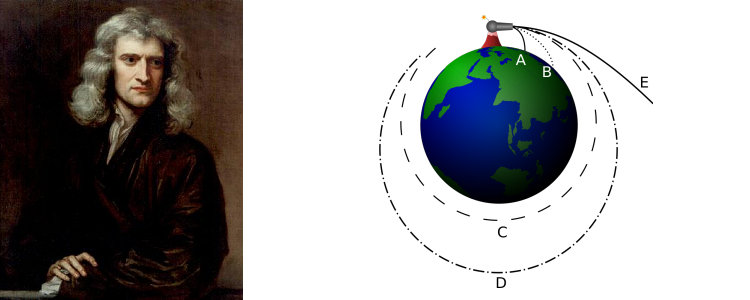
Isaac Newton avait compris que la force qui faisait tomber la pomme de l’arbre, était également responsable du fait que la Lune tournait autour de la Terre, et du fait que celle-ci et les autres planètes tournaient autour du Soleil. Tout comme la pomme, la Lune tombait sur la Terre. Mais, du fait de sa vitesse tangentielle, elle manquait continuellement notre planète, tout comme le ferait une bille tournant dans la cuvette de vos toilettes si elle ne subissait aucun frottement : elle continuerait à tourner indéfiniment autour du trou, sa trajectoire formant une ellipse. C’est exactement ce que font les planètes autour du Soleil, ou les satellites autour de leur planète. Je sais, j’ai pris un risque en comparant le système solaire à vos toilettes.
Voici une illustration un peu plus académique avec un canon maousse costaud dont les boulets se satellisent autour de la Terre.
Newton comprit également que cette force agissait avec la même intensité sur les deux objets en question, et que l’intensité de cette force était proportionnelle au produit des masses des deux objets, et inversement proportionnelle au carré de la distance les séparant.
Ne vous inquiétez pas : même si vous dormiez en cours de maths, au collège, je ne veux pas vous perdre. Pour saisir les deux choses que je viens d’énoncer, prenons l’exemple de la Terre et de la pomme.
La force qui attire la Terre et la pomme est d’autant plus importante que leur masse respective est importante (on multiplie les deux masses pour calculer cette force). Si une noix est quatre fois moins massive qu’une pomme, la force qui s’exerce entre elle et la Terre sera donc quatre fois moins importante que si c’était une pomme. Communément, cette force est appelée le poids : on dit que la noix pèse quatre fois moins qu’une pomme.
Mais pour calculer cette force, il faut aussi tenir compte de la distance séparant les deux objets (ou plus exactement séparant leur centre de gravité respectifs). Plus la distance sera grande, moins la force sera intense. Et cela selon le carré de cette distance (cette distance multipliée par elle-même). Autrement dit, si vous doublez cette distance, la force sera quatre fois moins intense. Et si vous quadruplez cette distance, elle sera seize fois moins intense. Inutile toutefois d’aller vous peser à l’étage plutôt qu’au rez-de chaussée, la différence de distance entre ces deux niveaux et le centre de la Terre étant hautement négligeable. Mais le fait est que vous pesez (microscopiquement) moins dans votre chambre que dans votre cave.
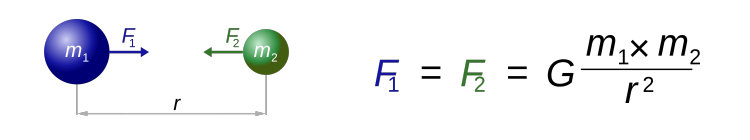
La seconde chose énoncée est que cette force agit avec la même intensité sur les deux objets (ici la Terre et la pomme). Et là vous me dites, c’est bien gentil mais quand une pomme tombe, la Terre ne fait pas un bond de deux mètres dans sa direction. Et vous avez raison. C’est ici qu’intervient l’inertie.
Prenez une batte de base-ball (ou un club de golf, ou un maillet de croquet si cela vous chante) puis disposez une boule de Bowling et une balle de Tennis sur le parquet de votre salon. Vous allez maintenant donner un bon coup dans la boule de Bowling. Vous constatez qu’elle se met à rouler tout doucement. Puis tapez, exactement avec la même force, dans la balle de Tennis. Vous constatez qu’elle file à toute vitesse… avant d’aller briser le service à thé que vous a offert votre grand-mère. Là, vous comprenez qu’une balle de Tennis peut être plus dangereuse qu’une boule de Bowling, mais vous saisissez aussi le fait que les deux objets n’ont pas eu le même comportement, alors même que vous leur avez appliqué la même force.
Lorsqu’une force agit sur un objet, cela a pour conséquence de modifier son mouvement, tant dans la direction que dans la vitesse. Mais ce changement de vitesse sera proportionnel à ce que l’on appelle la « masse inertielle » de cet objet. Plus sa « masse inertielle » sera grande, moins sa vitesse sera modifiée. Ceci est encore dû à Newton (dans ses lois de la Mécanique). Vous comprenez ainsi pourquoi la Terre, du fait de sa gigantesque masse inertielle, n’est quasiment pas affectée par l’attraction existant entre elle et la pomme (contrairement à cette dernière).
La notion de « masse » d’un objet recoupe donc deux concepts différents, agissant dans deux domaines différents :
- La « masse pesante » (ou « grave ») dont naît la force de gravitation entre deux objets.
- La « masse inertielle » intervenant dans le calcul du mouvement d’un objet soumis à une force.
Et ce qui est bluffant, c’est que ces deux concepts qui n’ont strictement rien à voir l’un avec l’autre, sont en fait… totalement équivalents. Si une balle de Tennis pèse, sur la balance, cent fois moins qu’une boule de Bowling, elle se déplacera cent fois plus vite qu’une boule de bowling soumise à la même force (ou, autrement dit, elle aura une inertie cent fois plus faible). La masse pesante est strictement égale à la masse inertielle. Et ni Newton, ni personne jusqu’au XXème siècle ne comprenait pourquoi on aboutissait à cette incroyable égalité. On pouvait juste la constater.
Notons au passage que c’est cette égalité qui, dans la théorie de Newton, permet à la noix, à la pomme, à la balle de Tennis et à la boule de Bowling de tomber au sol à la même vitesse (si l’on exclut le frottement de l’air). Les forces en jeu entre la Terre et ses objets sont certes différentes mais s’adaptent parfaitement à l’inertie de chacun de ces objets pour qu’au final, le résultat soit le même. Cette égalité entre masse pesante et masse inertielle apparaît un peu magique mais c’est ainsi.
Dans le même ordre d’idée, si vous remplacez la Terre par le service à thé de la grand-mère (cassé ou pas), vous constaterez que ce dernier suit la même orbite que la Terre autour du Soleil. La force qui « retient » la Terre est certes bien plus intense que celle qui « retient » le cadeau de Mamie, mais comme la masse inertielle du service de porcelaine est d’autant inférieure à celle de notre planète, tout se passe de la même manière. Magique.

Dernière remarque : cette force d’attraction, la gravitation, est super-méga-extrêmement faible. Il faut mettre en jeu des masses gigantesques (la Terre, par exemple) pour en déceler les effets. Cette force a beau s’exercer entre vous-même et tout ce qui vous entoure (stylo, écran, lustre, service à thé…), ses effets sont insignifiants.
Ultime dernière remarque, la Loi de l’attraction universelle de Newton, c’est vraiment de la balle ! C’est testé et ça fonctionne aussi bien dans votre salon qu’au niveau du système solaire. C’est ainsi qu’en notant, au XIXème siècle, quelques irrégularités dans l’orbite de la planète Uranus, on a pu, par de simples calculs issus de cette théorie, découvrir que ces perturbations s’expliquaient par la présence d’une autre planète un peu plus lointaine : Neptune. Oui, cette planète fut découverte en griffonnant des chiffres sur du papier. Bref, la gravitation de Newton, c’est vraiment de la balle ! Elle impose le respect, et qui oserait y toucher ?
La pensée la plus heureuse de sa vie
Nous sommes en 1907, deux ans après « l’année miraculeuse de la physique », « l’année d’Einstein »… qui n’est pour l’heure qu’une année intéressante (et encore uniquement du point de vue de quelques physiciens). D’ailleurs, Albert Einstein est demeuré simple fonctionnaire au Bureau des brevets de Berne. Mais bon, le cerveau continue de bouillonner, notamment du côté de ce qui allait devenir la physique des quanta. Il garde également à l’esprit son article sur la relativité, et il sait que ce pilier de la science qu’est la gravitation de Newton ne s’accorde pas très bien avec sa nouvelle théorie.
Pour Newton, la force de gravitation agit à distance et de façons instantanée entre deux corps. Or, depuis 1905, il sait que l’instantanéité est illusoire et qu’aucun signal, pas même une force, ne peut se propager plus vite que la lumière. Et puis cette action à distance ou encore cette équivalence « masse pesante / masse inertielle », toutes deux un peu « magiques », ne sont en rien expliquées par Newton. Et Albert, ça, ça le chatouille.
Bon, vous me direz que jusque là, la théorie de Newton n’a jamais été mise en défaut. Jamais ?… Pas tout à fait. Depuis une cinquantaine d’années, on avait en effet décelé une toute petite irrégularité dans l’orbite de la planète Mercure, celle qui est la plus proche du Soleil. Mais vraiment « toute petite ». Comme toutes les autres, l’orbite de cette planète décrit une ellipse autour de notre étoile. Et cette ellipse n’est pas fixe : elle tourne elle-même très lentement, au fil des siècles. Dit autrement, si vous prenez le point le plus proche du Soleil sur cette orbite (point que l’on appelle : périhélie), vous le verrez se déplacer au fil des siècles. C’est ce qui est montré ci-dessous de manière très très très exagérée (l’avance de ce périhélie en un siècle ne serait même pas décelable sur un tel schéma).
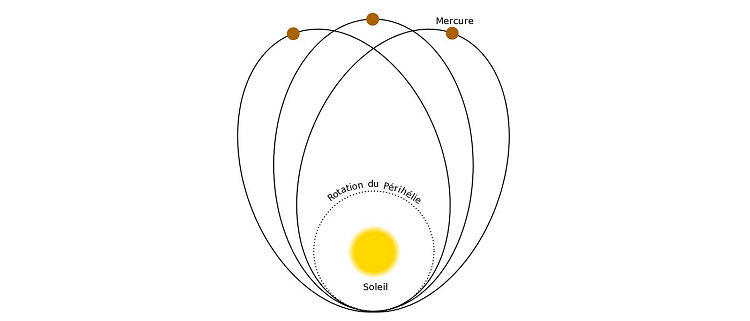
Et tout ceci est à nouveau expliqué par la théorie de Newton en tenant compte des interactions avec les autres planètes… à un chouia près. Entre le calcul et ce que l’on observe, il y a une microscopique différence : 43 secondes d’arc, c’est à dire l’angle correspondant à l’épaisseur d’un cheveu à un mètre de distance !… Oui, c’est peu. Et cela par siècle !
Mais cela n’a beau être qu’un chouia, ce n’est pas rien. Comme pour Uranus, on a bien tenté de chercher une hypothétique planète inconnue encore plus proche du soleil pour expliquer cela. Sans résultat. On a aussi évoqué un nuage de poussières, de gaz. En vain… Mais bon, ce n’était qu’un chouia, et on allait bien finir par trouver une explication. Et ça aussi, Einstein le savait.
Mais le vrai déclic intervint un jour de 1907 où, assis sur sa chaise de bureau, il eut une pensée qu’il allait, plus tard, qualifier de « pensée la plus heureuse de ma vie ». Elle ne semble pourtant n’avoir aucun caractère extraordinaire, même d’un point de vue physique. On peut résumer cette pensée par : si une personne est en chute libre, elle ne ressent pas son propre poids. En d’autres termes, en chute libre, en étant pleinement soumis à la gravitation, celle-ci semble disparaître.
En effet, mettez-vous en situation : transportez-vous dans un ascenseur tout en haut de l’Empire State Building, et imaginez que les câbles de l’ascenseur lâchent. Abstenez-vous de hurler, et observez plutôt la scène : vous flottez dans l’ascenseur avec votre sac, votre parapluie. Vous semblez en apesanteur, vous ne ressentez aucune accélération. Vous ne ressentez pas la force qui est censée être la cause de votre chute.
Pour Newton comme pour les physiciens de 1907, cela est normal : c’est une illusion due au fait que l’ascenseur, vous-même et tout ce qui vous entoure, tombez à la même vitesse (accélérée) en étant soumis à la force de gravitation. Pour Einstein, c’est un indice de taille (pour ne pas dire de poids) : si vous ne ressentez pas cette force, existe t-elle réellement ?
Cette pensée concernant la chute libre, fait tressaillir Einstein. Il sait à présent quelle est la voie à suivre. Oui, c’est bien la pensée la plus heureuse de sa vie.
Un nouveau principe d’équivalence
Et ses interrogations vont l’amener à élaborer un nouveau principe d’équivalence. Voyons à quoi cela ressemble. Reprenons notre laboratoire clos et insonorisé, à l’intérieur duquel vous vous réveillez. Là, pas d’apesanteur : vous êtes bien collé au sol. Vous vous dites donc que vous êtes sur Terre, et que vous êtes soumis à la gravitation… Mais imaginez que votre laboratoire ait été placé dans une fusée au milieu de l’espace interstellaire, et que c’est l’accélération continue du moteur de cette fusée, placé sous votre plancher, qui vous plaque ainsi au sol. Einstein pense qu’il vous est impossible de déterminer votre situation, quelle que soit l’expérience que vous feriez dans ce laboratoire. Voilà, c’est ça le nouveau principe d’équivalence.
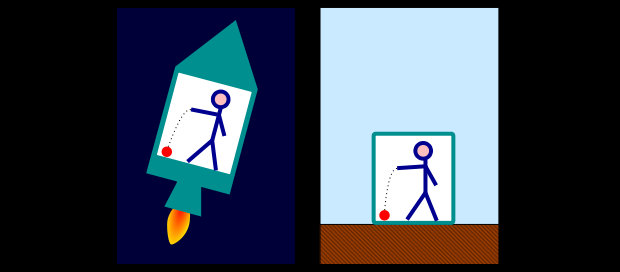
Aussitôt Newton intervient, et vous dit que vous pouvez tout à fait déterminer votre situation. C’est même très simple. Vers une cible sur le mur, dirigez un faisceau lumineux voire, pour faire plus simple, un faisceau laser (oui, mon Newton connaît les ascenseurs, les fusées et le laser, et ne m’ennuyez pas avec ça). Du fait de l’accélération de la fusée et du temps mis par la lumière dans son trajet vers le mur, le point de mon laser va aboutir un peu en dessous de la cible. Le faisceau lumineux semble courbé par l’accélération de la fusée (même s’il faut une accélération colossale pour que cela puisse être détectée, la vitesse de la lumière étant tout aussi colossale). Jusque là, tout le monde est d’accord. Et c’est là que Newton balance son argument massue : la lumière n’a pas de masse et n’est donc pas soumise à la loi de la gravitation. Et donc, sur Terre, le faisceau de lumière ne sera pas courbé, et le point laser sera pile sur la cible. Les deux situations ne sont donc pas symétriques. CQFD.
Et là, Einstein nous dit qu’il a l’intuition que son principe d’équivalence est vrai, que le rayon de lumière sera courbé dans tous les cas. Et donc que Newton a tort. Et qu’il va nous expliquer pourquoi.
Cela va prendre huit ans.
Une nouvelle théorie de la gravitation
Comme on en a pris l’habitude avec Einstein, le principe de base qui va mener à sa théorie, renverse toutes les idées préconçues de son époque (dont la plupart surnagent encore dans votre cerveau… si, si). Et là, je dis, avec plus d’assurance qu’un Steve Jobs : c’est une ré-vo-lu-tion !
En partie, cela s’appuie bien évidemment sur la théorie de la Relativité restreinte qui, deux ans auparavant, avait transfiguré les concepts d’espace et de temps. Si auparavant, espace et temps constituaient un cadre fixe, éternelle, immobile, telle une simple scène à l’intérieur de laquelle se jouait l’histoire de l’univers, ils avaient, depuis 1905, pris place au sein de la pièce. De même, le fait que toute modification de l’un entraînait une modification équivalente de l’autre, comme si de l’espace se transformait en temps et inversement, avait permis, d’un point de vue mathématique, de les réunir en un seul concept : l’espace-temps.
Mais les étirements de cet espace-temps pouvaient encore apparaître comme des effets de perspective. Ici, ils vont prendre une réelle consistance, et faire de ce concept mathématique, un véritable objet physique.
Quant à la masse qui était au centre de la théorie de Newton, elle laisse ici sa place à l’énergie (E=mc² est passé par là). La masse demeure toutefois le principal réservoir de cette énergie qui va entrer dans la danse. Mais aucune force, au sens où vous l’entendez, n’animera cette danse.

Allez, on plonge… L’idée d’Einstein n’est pas si complexe que cela, même si elle demande un (gros) effort d’imagination.
Selon la Mécanique de Newton, toute particule (ou objet si vous préférez) qui n’est soumise à aucune force (ou soumise à des forces qui s’annulent entre elles) demeure immobile. Chacune a sa propre immobilité qui, pour d’autres, correspond à un mouvement rectiligne uniforme (un mouvement en ligne droite sans accélération). Ce n’est rien d’autre que l’histoire du gars sur le quai qui se dit immobile par rapport au train passant devant lui, et de son ami dans le train affirmant que c’est lui qui est immobile, le quai et le paysage défilant devant lui. Tous deux ont le droit de se dire immobile comme on l’a vu dans les précédents « épisodes ».
En d’autres termes, si vous vous imaginez flottant dans l’espace interstellaire, vous allez observer ces particules (ou parapluies, ou planètes) filer, dans toutes les directions, en ligne droite à vitesse constante (dans leur immobilité à elles). Pour Newton, c’est ici qu’intervient la force de gravitation, agissant entre chacune de ces particules du fait de leur masse (et rappelons-le : il faut une grande masse en jeu pour que l’effet soit perceptible). Cette force va donc modifier les trajectoires de ces particules, c’est à dire les incurver, les accélérer, les freiner.
Selon Einstein, ce n’est pas ce qui se passe. L’énergie de ces particules (essentiellement la masse) va modifier la structure de l’espace-temps. Pour mieux comprendre, imaginez une gigantesque toile de nylon représentant l’espace-temps, et des billes de toutes tailles, dont des boules de billard, de bowling, roulant en tous sens sur cette immense toile. Ces billes agissent sur cette dernière comme les particules agissent sur l’espace-temps, en la courbant. Et vous comprenez tout de suite que les trajectoires de tous ces éléments vont être déformées. Si la trajectoire d’une bille passe à proximité d’une boule de billard, elle sera déviée du fait de la courbure de la toile à cet endroit. Elle sera encore plus déviée en passant près d’une boule de bowling. Si la bille passe très près, et si elle ne va pas trop vite par rapport à la boule de bowling, il y a de grande chance pour que sa trajectoire se referme sur elle-même, et qu’elle se mette à tourner autour, comme une planète autour du Soleil. Enfin, si elle passe vraiment trop près et que sa vitesse est vraiment trop lente, la rencontre entre la bille et la boule devient inévitable.
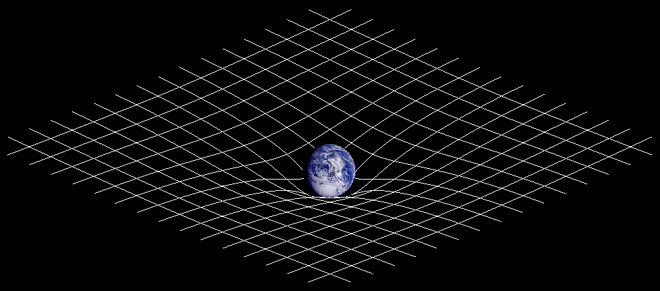
L’analogie entre l’espace-temps et la toile est souvent utilisée pour vulgariser la Relativité générale, mais peut entraîner quelques malentendus. Il faut bien comprendre que les billes ne sont pas entraînées vers le fond de la cuvette par leur poids, ce qui reviendrait à réintroduire la gravitation de Newton. Non, ce sont les trajectoires qu’elles suivent, les « lignes droites » qu’elles parcourent, qui se trouvent courbées parce que leur support (la toile ou l’espace-temps) est lui-même courbé.
En géométrie, ces trajectoires sont appelées des géodésiques. Elles ont pour propriété de représenter le plus court chemin d’un point à un autre. Dans un espace euclidien, c’est à dire l’espace tel que vos sens l’imaginent, le plus court chemin d’un point à un autre, c’est une ligne droite.
Et quand Newton nous dit qu’un objet qui n’est soumis à aucune force, va en ligne droite, on devrait plutôt dire qu’il suit une géodésique. Ce que pense Einstein n’est guère éloigné. La grosse différence est que, pour lui, notre espace n’est pas euclidien : il est déformé par la masse et l’énergie cinétique des objets qui s’y trouvent. De ce fait, les géodésiques ne sont plus des lignes droites mais des courbes, voire des trajectoires encore plus biscornues.
En outre, dans un espace euclidien comme celui de Newton, peu importe la vitesse avec laquelle nous nous rendons d’un point à un autre par le plus court chemin. Ce plus court chemin demeure identique. Ici, non : les géodésiques diffèrent.
Enfin, dans cet espace d’Einstein, cet espace non-euclidien, les géodésiques peuvent non seulement se courber mais également s’étirer ou se rétracter, donnant l’impression que l’objet accélère ou décélère plutôt que d’adopter une vitesse constante.

Bref, vous avez compris que, pour Einstein, ce que l’on appelle la force de gravitation, n’est en fait qu’un effet géométrique dû à la déformation de l’espace et du temps.
La station spatiale internationale et la Lune ne sont soumises à aucune attraction gravitationnelle de la part de la Terre. Elles ne sont soumises à aucune force : elles continuent d’aller tout droit. Mais c’est l’espace-temps, déformé par la Terre, qui fait que la géodésique qu’elles suivent, boucle autour de la Terre, un peu comme ces motos de foire qui foncent tout droit sur des anneaux leur servant de piste.
De même, dans votre ascenseur en chute libre, vous n’êtes soumis à aucune force : vous suivez tout naturellement votre géodésique… qui, malheureusement pour vous, passe par le sol. Et si vous semblez accélérer, bien que vous ne ressentiez rien, c’est que votre géodésique suit la « courbure » appliquée à l’espace par la Terre. Vous parcourez plus d’espace par unité de temps parce que votre géodésique s’étire.
Même, là, assis sur votre chaise, n’étant soumis à aucune force, votre corps ne peut que suivre sa géodésique, tout comme la Terre suit la sienne. Et là, c’est son inertie contre la vôtre (et vous ne faites pas le poids, si j’ose dire).
Bon, ne le cachez pas, vous avez du mal à vous représenter tout cela. Qu’est-ce que c’est que cet « espace courbe » ? Dites-vous déjà que les qualificatifs de « courbe » ou de « plat » sont empruntés à l’analogie de la toile en nylon. Mettons-les de côté.
Ce qu’il faut bien comprendre, c’est que depuis Einstein, l’espace (et ce sera la même chose pour le temps) n’est plus quelque chose d’inerte, n’est plus la simple scène fixe et éternelle où surviennent les événements physiques. Il vous faut faire un effort de conceptualisation, et imaginer que l’espace et ses longueurs peuvent se contracter ou se rétracter, comme s’il s’agissait d’un bloc de gélatine au sein duquel nous évoluerions. Dans un tel espace, les règles de la géométrie euclidienne que vous aviez apprises dès l’école élémentaire (pi et le cercle, les sommes des angles d’un triangle, les parallèles qui ne se croisent jamais, etc.) deviennent fausses. Ainsi, une courbe entre deux points peut être ici plus courte qu’une ligne droite (s’il le faut, relisez plusieurs fois cette phrase).
Et ce qui déforme cet espace, c’est la densité d’énergie (en grande partie, de masse) qu’il contient à tel ou tel endroit.
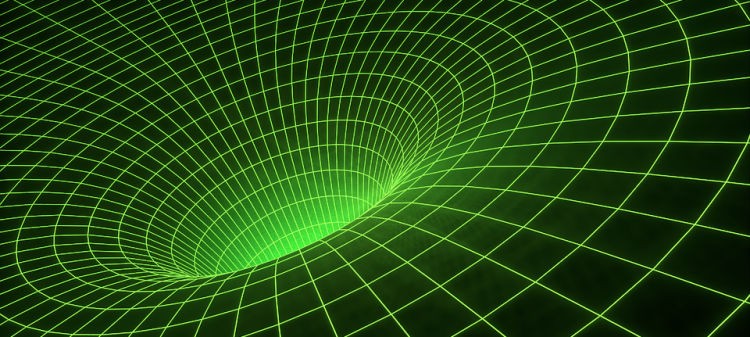
Voici une illustration vidéo de cette déformation de l’espace…
Et il en est de même pour le temps. Dans cette théorie, la vitesse à laquelle tournent les aiguilles d’une montre, dépend aussi des différentes densités de masse-énergie. Ce n’est pas uniquement l’espace qui est « courbé », c’est l’espace-temps (et l’influence de la composante temporelle sur les géodésiques est sans doute la plus importante). Ainsi, à la surface du Soleil, les aiguilles d’une montre qui n’aurait pas fondu, tourneraient moins vite qu’à la surface de la Terre, et ceci du seul fait de la différence de masse entre les deux astres. Ceux qui auront vu le film Interstellar (même s’il est un peu maladroit et excessif dans ses exemples) sauront de quoi nous parlons : les secondes vécues à tel endroit, peuvent être des années à un autre endroit.
N’oubliez pas non plus le principe d’équivalence, et l’accélération de votre fusée qui, comme un champ gravitationnel, ne sera pas non plus sans effet sur l’espace-temps : souvenez-vous des jumeaux de Langevin que nous avions évoqués dans le quatrième article (l’un des deux revenant de son voyage tout fringant pour aller fleurir la tombe de son frère, mort de vieillesse cinquante ans auparavant).
Tout ceci n’est pas une fantaisie de physicien chevelu : il s’agit bien de votre univers, de l’espace au sein duquel vous évoluez, de votre montre. En établissant cette théorie, Einstein vous invite à rompre avec tous vos repères, avec tout ce que vos sens ont établi pour sûr. L’espace et le temps tels que vous les imaginiez ne sont que des artefacts. Si vous commencez à ressentir cela, le vertige n’est pas loin.
Il faut aussi comprendre qu’au-delà de la question de la gravitation, cette théorie a des répercussions sur des thèmes qui semblaient, jusqu’alors, relever de la métaphysique. Ainsi, Einstein établit une relation intime entre, d’une part, la matière, l’énergie, et d’autre part, l’espace et le temps. C’est la matière, l’énergie qui donne ici une consistance à l’espace et au temps. C’est l’énergie qui, si j’ose dire, leur donne vie.
Avec Newton, on peut tout à fait imaginer ce que serait un univers vide, un espace ne contenant rien, et un temps sans montre. Ce serait ennuyeux comme une scène de théâtre désertée… mais on peut l’imaginer.
Avec Einstein, un univers vide n’a plus de sens, car sans matière, sans énergie, les concepts d’espace et de temps perdent toute réalité. Cette théorie, nous dit par exemple que les aiguilles d’une montre ralentissent quand la densité de masse-énergie augmente. D’une certaine façon, on pourrait dire que cette masse-énergie « retient » le temps. Mais dans un univers vide, que devient le temps qui n’est plus « retenu » ? Et c’est la même chose pour l’espace qui est « contraint » par l’énergie qu’il contient. Sans elle, deux points contigus seraient tout à la fois infiniment séparés. Dans un univers vide, les notions d’espace et de temps n’ont plus aucun sens. Un univers vide n’a plus de réalité.
Je vous laisse réfléchir à tout ceci mais n’ayez aucun doute, c’est puissant.
Un chantier de huit ans
Entre l’intuition de 1907 (qui ne correspondait pas à tout ce que je viens de décrire) et la publication définitive de cette théorie, près de huit années vont s’écouler.
En effet, si l’idée générale peut s’expliquer avec des mots ainsi que je me suis hasardé à tenter d’essayer de croire y parvenir (et encore…), les équations qui gouvernent cette nouvelle théorie ne sont pas simplement ardues à édicter, elles constituent une chaîne de montagnes de difficultés.
Il s’agit en effet de mettre en équation le comportement de la matière et plus généralement de l’énergie, qui va influer sur un espace-temps, comportant donc quatre dimensions, et qui, lui-même, modifiera le comportement de cette matière, de cette énergie. Et tout ceci en respectant un principe de relativité affirmant que les lois de la physique doivent prendre les mêmes formes mathématiques dans tous les référentiels. Ouch… Et encore faut-il vérifier que cela fonctionne.
Certains des outils mathématiques nécessaires à la réalisation de ce projet sont assez récents pour l’époque, notamment concernant la géométrie non euclidienne. D’autres vont tout simplement devoir être créés. Je vous rassure : nous n’allons pas parler de « champs tensoriels définis sur une variété pseudo-riemannienne » car, même si je trouve cela très joli à écrire, je n’y comprend pas grand chose de plus que vous. Pour ceux qui voudraient vraiment en savoir plus, vous vous êtes trompés de blog (mais vous pouvez aller sur Wikipedia ou, plus sympathiquement ici).
Contrairement à une légende urbaine, Albert Einstein touche sa bille en mathématiques, et pas un peu. Mais, en 1912, après avoir cru être proche de la solution, il doit se résoudre à demander de l’aide (il comprend que l’espace-temps ne peut posséder qu’une géométrie non euclidienne). Cette aide, il va aller la rechercher auprès de l’un de ses anciens amis de l’École polytechnique de Zürich : le Hongrois Marcel Grossmann (ci-dessus avec Albert). Ce dernier lui apporte les outils pour maîtriser les champs de tenseurs (de curieux animaux que nous ne décrirons pas). Même si Grossmann n’est pas toujours convaincu par l’interprétation physique que fait Einstein de ces outils, leur collaboration dure jusqu’en 1913. Elle s’avère fructueuse mais de nombreuses difficultés demeurent.
Einstein poursuit seul, en communiquant régulièrement sur l’avancée de ses travaux, et en tenant compte des avis de ses condisciples. « Condisciples » car, entre temps (en 1909), il a enfin eu un poste universitaire à Prague puis a fini par rejoindre l’Académie des sciences de Prusse, à Berlin (en exigeant de conserver sa nationalité suisse). Toutefois, si certains l’encouragent, à l’image d’Hendrik Lorentz, à poursuivre sur cette voie, la plupart des physiciens demeurent sceptiques. Ce n’est en tout cas pas le cas du mathématicien allemand David Hilbert (ci-dessous) qui invite Einstein à faire une conférence sur ce sujet en juin 1915.

Fin novembre 1915, après avoir communiqué à trois reprises, chaque semaine, sur l’aboutissement de ses travaux, Albert Einstein, aussi exténué qu’un marathonien, livre son manuscrit final. David Hilbert l’a précédé de quelques jours en soumettant un article aboutissant à la même équation du champ gravitationnel, en suivant un raisonnement quelque peu différent. Mais Hilbert, soulignant qu’il s’était référé aux travaux d’Einstein, ne contestera à aucun moment la paternité du physicien sur cette théorie.
La théorie de la Relativité générale est officiellement publiée le 2 décembre 1915. L’Univers jubile mais la Terre qui est en guerre, une effroyable guerre, n’en sait rien.
Mise à l’épreuve de la théorie
Si, par son formalisme mathématique, la théorie d’Einstein peut apparaître autrement plus complexe que celle de Newton, elle prend le pas sur cette dernière en décrivant une réalité physique bien plus globale, bien plus fondamentale, et en possédant une logique interne bien plus simple, sans recours à de mystérieux hasards tel que l’était l’égalité entre masse pesante et masse inertielle.

Si cette nouvelle théorie aboutit à des résultats différents par le fait qu’elle prend en compte l’énergie et non la seule masse, et que, par exemple, la rotation d’un objet entraîne une déformation de l’espace-temps, ce qui était sans effet chez Newton, il n’empêche que la loi édictée par ce dernier demeure une très bonne approximation de la Relativité générale, et c’est pourquoi elle continue d’être largement utilisée, même pour calculer les trajectoires des sondes interplanétaires. En fait, on n’a recours à la Relativité générale que si l’on a besoin d’une extrême précision ou si l’on s’intéresse à des champs gravitationnels exceptionnellement intenses. C’est donc dans ces domaines que l’œuvre d’Albert Einstein sera mise à l’épreuve.
L’anomalie du périhélie de Mercure
Dans la foulée de la publication de sa théorie en novembre 1915, Albert Einstein fournira le calcul de l’avancée du périhélie de Mercure. Certains, notamment Hilbert, s’étonnèrent de la rapidité avec laquelle il avait pu établir ce calcul. Comme Etienne Klein l’indique (dans l’une des vidéos que je vous proposerai plus bas), on a compris récemment qu’il avait déjà procédé à ce calcul en 1913. Avec un résultat totalement aberrant, et ce en raison d’une mauvaise piste suivie, d’un mauvais outil mathématique préféré à celui proposé par Marcel Grossmann, qu’il jugeait moins esthétique. L’esthétisme tient une grande place dans le mode de fonctionnement intellectuel d’Einstein. Dans ce cas précis, cela l’aura desservi, un temps.
Mais peu importe, deux ans plus tard, contrairement à la Loi de Newton (et son défaut de 43″ d’arc), la Relativité générale s’avère, cette fois-ci, en parfait accord avec l’observation. Il racontera à un ami comment l’obtention de ce résultat l’avait plongé dans une transe qui aurait pu lui être fatale. Le mystère de l’anomalie du périhélie de Mercure était résolu. Einstein venait de prendre le pas sur l’immense Newton.
L’éclipse d’Eddington
Vous vous souvenez que la Relativité générale prévoyait la déviation des rayons lumineux. C’est un astrophysicien anglais, Arthur Eddington qui allait mettre en évidence cet effet à l’occasion d’une éclipse de Soleil, le 29 mai 1919. La théorie prévoyait que la lumière d’une étoile passant à proximité du Soleil devait être très légèrement déviée par la masse de ce dernier, selon un angle parfaitement déterminé par les équations d’Einstein. Le problème était bien sûr de pouvoir observer une étoile avec, dans le ciel, le Soleil tout à côté. D’où l’intérêt de cette éclipse qui devait se produire dans l’Atlantique-Sud, et que l’Anglais n’allait pas manquer en embarquant, avec son matériel astro-photographique, vers Sao-Tomé (photographies ci-dessous).

La nouvelle ne tarda pas à parvenir en Europe, et à faire le tour du Monde. Marge d’erreur mise à part, l’étoile apparaissait bien avec la déviation calculée : la Relativité générale triomphait. Et pour un triomphe, c’en fut un ! La presse mondiale (si l’on excepte la presse française, en grève) se fit l’écho de ce succès, et l’engouement fut général ! Un incroyable enthousiasme qui en étonna beaucoup, et tout particulièrement Albert Einstein, propulsé méga star du genre humain.
C’est de ce jour que date la popularité de notre physicien ébouriffé. Comment l’expliquer ? Il y a bien sûr l’aura de mystères – savamment entretenue par les journaux – qui entourait cette découverte révolutionnaire mais peu évidente à vulgariser. Il y a aussi la personnalité atypique d’Albert Einstein, drôle, espiègle, généreux, que saura utiliser la presse. Et il y a surtout le contexte : à peine sorties de la boucherie du premier conflit mondial, les populations ne rêvaient que de paix universelle et d’avenirs radieux. Voir un anglais, pacifiste notoire, confirmer la validité d’une théorie « allemande », constitua un véritable symbole d’espoir et de renouveau. Ceci fut sans doute aussi la cause d’une explosion des vocations chez quelques génies en herbe qui, les années suivantes, allaient faire parler d’eux (mais on causera des quanta, une autre fois).
Un univers non stationnaire
La Relativité générale allait vite rencontrer un premier écueil. On se rendit compte que ses équations impliquaient que l’espace-temps était instable : il devait se contracter ou se dilater. Il n’avait aucune raison d’être pile-poil à l’équilibre. Or, à cette époque, il était évident pour tous que l’univers était stationnaire, qu’il avait toujours été et qu’il serait pour toujours tel qu’on pouvait l’observer.
Le seul moyen de résoudre cette absurdité fut donc, pour Einstein, en février 1917, d’ajouter un nouveau terme à ses équations. Un terme qu’il allait nommer « constante cosmologique » et qui permettait de rendre sa stabilité à l’univers. C’était un procédé assez artificiel. Il n’avait pas aimé faire cela, mais c’était le prix à payer pour sauver l’échafaudage qu’il avait si durement bâti.

Dix ans plus tard, la fuite des galaxies était découverte. On ne tarda pas à comprendre l’impensable : l’univers n’était pas stationnaire, il était en expansion !
Chose incroyable : la possibilité du Big Bang et de ses avatars était incluse dès l’origine dans la théorie d’Einstein… ce qu’il s’était refusé à comprendre. Il qualifiera plus tard sa constante cosmologique de « plus grande bêtise de ma vie ». La Relativité générale avait même eu raison contre son propre créateur. On peut difficilement faire mieux.
Notez qu’Einstein serait surpris de savoir que sa constante cosmologique a été récemment ressuscitée. Mais c’est une autre histoire d’énergie, très sombre, que l’on évoquera un peu plus bas.
Quant au Big Bang, si cela vous intéresse, n’hésitez pas à découvrir la série d’articles qui y sont consacrés sur Carb.one.
Une singulière singularité
Une difficulté allait à nouveau surgir, et menacer bien plus sérieusement l’édifice de la Relativité générale, au point de lui faire perdre une grande part de sa crédibilité pour un bon nombre d’années.
A l’origine, il y a un soldat allemand (et physicien), Karl Schwarzschild, qui, en pleine guerre mondiale, va se passionner pour les travaux d’Einstein. Il sera le premier, dès la fin de 1915, à proposer (et à envoyer à Einstein) une solution des équations de la Relativité générale concernant la géométrie de l’espace-temps autour d’un objet sphérique (cas simple d’une étoile sphérique qui ne serait pas en rotation). Einstein, admiratif, présentera les calculs de Schwarzschild à son Académie prussienne dès janvier 1916. Ces calculs auront un grand impact dans le développement de nos connaissances sur l’univers. Quant à leur auteur, il ne survivra pas au printemps : il mourra en mai 1916 d’une maladie contractée sur le front russe.
L’élégance des calculs de Schwarzschild vont effectivement permettre de grandes avancées en matière d’astrophysique. Mais certains, comme le mathématicien français Jacques Hadamard, s’en serviront pour prouver à Einstein qu’il y a bien quelque chose qui cloche dans sa théorie : pour un certain rayon, fonction de la masse de l’objet, l’équation s’effondre, c’est à dire que la courbure de l’espace devient infinie et le temps s’arrête. C’est ce que l’on appelle une singularité, et ce n’est pas bon du tout pour une théorie. En d’autres termes, on a trouvé un cas où l’équation devient folle. Et pour la plupart des physiciens, cela revient à dire que l’on a trouvé un cas où l’équation devient fausse… et que, par extension, toute la théorie devient fausse. Rares sont ceux ceux qui, comme l’Indien Subrahmanyan Chandrasekhar, vont y voir une réalité physique.
De son côté, pour sauver les meubles, Einstein tentera d’expliquer qu’aucun objet physique ne peut être réduit à ce rayon, que l’on nommera « rayon de Schwarzschild » (cela reviendrait, par exemple, à condenser toute la masse du Soleil dans un rayon de seulement 3km). L’impossibilité mathématique se heurterait à l’impossibilité physique. Ce raisonnement ne convainquit pas grand monde : la Relativité générale fut boudée durant des décennies, et Einstein n’obtint pas le Prix Nobel pour sa théorie (il en obtiendra tout de même un pour sa contribution à la physique quantique).
Il faudra attendre les années 60 et de grands progrès en astrophysique (avec la quasi certitude qu’un astre pouvait atteindre le rayon de Schwarzschild) pour que plusieurs physiciens (en premier lieu, l’Anglais Roger Penrose) remettent en pleine lumière la Relativité générale. Ils démontrèrent que, si l’équation paraissait folle, elle n’était pas pour autant fausse. Elle décrivait en fait des objets très exotiques et qui allaient connaître un grand succès, tant scientifique que médiatique : les trous noirs !
Suivront les premières indications observationnelles en faveur de leur existence, et l’aspect théorique sera ensuite affiné par des gens comme Stephen Hawking ou Jean-Pierre Luminet. Mais c’est une autre histoire que nous conterons plus tard.
Notons que c’est à la même période que la théorie du Big Bang triomphera. Loin d’être mise au rencart, la Relativité générale connaît alors son âge d’or !
Des décalages, mirages et vagues gravitationnelles
Dès lors, les succès de la Relativité générale vont se succéder.
L’influence de la théorie sur le temps – le fait que les aiguilles des horloges ralentissent à mesure que se creuse la courbure de l’espace-temps – a été vérifié dès 1959 (expérience de Pound-Rebka à Harvard). Ce décalage temporel fait d’ailleurs partie de votre quotidien, tout comme les effets de la Relativité restreinte, car si l’on ne les prenait pas en compte, le système GPS (basé sur des horloges placés en orbite) aurait une précision non pas du mètre mais de l’ordre du kilomètre. Les vacanciers apprécieront. La Relativité générale, c’est aussi du concret.
C’est du concret mais c’est également la beauté des grands espaces. La théorie d’Einstein prévoit en effet que l’espace-temps, courbé par une masse considérable, peut agir comme une lentille en déviant la lumière d’objets situés en arrière-plan. Ce peut être une galaxie ou un amas de galaxies autour duquel vont apparaître déformés des galaxies bien plus lointaines (notamment des quasars), situées sur la même ligne de visée, et qui, bien souvent, n’auraient pas été assez lumineuses pour être détectées.
Le premier exemple de ce type de mirages sera observé en 1979 sous la forme d’un arc lumineux. Depuis, ils ne cessent de se multiplier. Voici un exemple sous forme d’anneau (appelé « anneau d’Einstein ») déniché par le télescope spatial Hubble…

D’autres tests réussis de la Relativité générale existent (décalage vers le rouge de la lumière dans un champ gravitationnel, évolution de l’orbite d’un pulsar binaire) mais terminons avec le dernier en date, et pas le moindre : la détection directe des ondes gravitationnelles, annoncée officiellement le 11 février 2016, cent ans après qu’Albert Einstein les ait prédites.
Il s’agit d’ondulations de l’espace-temps – comme les vagues sur l’eau – produites par des corps massifs accélérés. Dans les faits, pour que ces ondes aient une chance d’être détectées avec les moyens techniques dont nous disposons, il ne peut s’agir que d’événements cataclysmiques, à l’image d’une pierre tombant au milieu d’un lac… Enfin un « lac cosmique ». Concrètement, il s’agit de deux trous noirs entamant une danse effrénée se concluant par une étreinte fatale.
Voici une reconstitution par ordinateur de l’événement observé par le détecteur LIGO (sachez que ce que vous voyez, ne dure en fait qu’un tiers de seconde, et notez la prise en compte des déformations de l’espace temps faisant tourner le fond d’étoiles en arrière-plan).
Pour se rendre compte de l’exploit, sachez que ce qui a été détecté, c’est une longueur de 4km parcourue par un laser qui s’est déformée d’un milliardième de milliardième de mètre. C’est très petit petit petit, quelque chose de l’ordre d’un cent-millionième de la taille d’un atome !… C’est petit mais c’est énorme : un siècle après les avoir imaginées, le génie d’Einstein continue de faire des vagues. Et tout ceci ouvre sans doute la voie à une nouvelle astronomie, non plus lumineuse mais gravitationnelle.
La Relativité générale aujourd’hui
Soyons clairs : la théorie d’Einstein n’a jamais été prise en défaut, chaque faille que l’on pensait avoir trouvée l’ayant, au final, renforcée.
Il y a bien eu des anomalies détectées dans les trajectoires de sondes Pionner aux confins du système solaire – une infime et anormale décélération – mais, après des tests concluants en 2012, la communauté scientifique s’accorde, aujourd’hui, sur une explication prenant en compte la chaleur des générateurs de ces sondes dont le rayonnement serait réfléchi par leur antenne.

Donc rien… Et c’est bien ennuyeux pour cette même communauté scientifique.
Ennuyeux tout d’abord par le fait que la Relativité générale n’offre aucune réelle piste de recherche concernant deux phénomènes mis en évidence ces dernières années, et que nous aurons l’occasion d’évoquer dans un prochain article :
- La « matière noire » (ou « sombre »)
Qu’il s’agisse de la rotation d’une galaxie, ou de la dynamique d’un amas galaxies, les mouvements observés ne correspondent pas aux calculs : la masse, c’est à dire la matière que l’on observe, ne suffit pas à expliquer ces mouvements. Tout se passe comme si une part importante de la matière (plus des quatre cinquièmes, excusez du peu) demeurait invisible à nos yeux. - L’« énergie sombre » (ou « noire »)
C’est avec stupéfaction que l’on découvrit, en 1998, que l’expansion de l’univers, loin de se ralentir, s’accélérait. Et l’énergie nécessaire à cette accélération correspond à près de 70% de l’énergie totale de l’univers, matière (ordinaire ou noire) comprise. Et on ne sait rien de cette énergie. Tout juste peut-on la « matérialiser » en Relativité générale en ressuscitant la constante cosmologique de 1917.
S’agit-il là de nouvelles « anomalies du périhélie de Mercure » qui déboucheront sur une nouvelle théorie de la gravitation, ou est-ce la mise en évidence d’une nouvelle forme de matière, et d’une force inconnue ? A ce jour, le débat reste ouvert.

Enfin, un dernier argument – sans doute le plus sérieux – nous amène à penser que la Relativité générale ne constitue pas la théorie ultime de la gravitation. Et cela, on le doit au second pilier de la physique moderne : la physique quantique, une théorie qui a connu encore plus de succès que la Relativité générale, et qui englobe bien plus de choses (dont nous ne parlerons surtout pas aujourd’hui).
Le problème est que ces deux théories se révèlent physiquement incompatibles : deux visions inconciliables du Monde. Le chantier demeure donc gigantesque, et la nature, couronnant de succès ces théories, ne nous offre que peu d’indices. Le travail avance (théories des cordes, gravitation quantique à boucles, et autres). Aboutira t-il ? Y aura t-il un nouveau Newton, un nouvel Einstein pour nous faire découvrir des horizons insoupçonnés ? Seul l’avenir nous le dira.
Une chose est sûre : même si je viens d’en terminer (pfffiouuuuu) avec cette série d’articles sur la relativité, la curiosité reste de mise !
Bonus Vidéos
Comme à l’habitude, voici quelques vidéos sur le sujet, susceptibles de vous intéresser (mais pensez aussi à la lecture, avec par exemple le livre Albert Einstein, créateur et rebelle de Banesh Hoffmann au Seuil… s’il est encore édité).
Conférence d’Etienne Klein à l’IFG
Etienne Klein : Si la relativité générale m’était contée… (CEA)
La Relativité générale présentée sur la chaîne E-penser
Les ondes gravitationnelles présentées sur la chaîne ScienceEtonnante
La relativité
- Partie 1 : ce n’est pas absolu
- Partie 2 : c’est l’égalité
- Partie 3 : ça se contracte
- Partie 4 : c’est révolutionnaire
- Partie 5 : c’est aussi « E= mc² »
- Partie 6 : c’est général





bonjour, a la lecture de ces échanges, il est ecrit de nombreuses fois, « la pomme ou autre suit sn géodésique ».
Mais pourquoi vers la terre, et pourquoi pas dans l’autre sens?
Merci de votre regard sur cette question
Bonjour,
Merci pour toutes ces explications concernant la RG; je me permets ce commentaire car l’histoire de la pomme en RG n’est pas encore complètement claire pour moi.
J’ai compris qu’en RG, lorsque la pomme est accrochée à l’arbre, elle est tirée par le haut par l’effet de la force électromagnétique. Puis, quand elle quitte l’arbre, elle se retrouve au repos.
Mes questions sont les suivantes:
1. Est-ce la force EM – qui induit une accélération vers le haut – qui attire la pomme vers la Terre lorsque elle quitte le pommier et se retrouve au repos ? Si oui, s’agit-il essentiellement de la force EM de la Terre?
2. dans ce cas, la déformation de l’espace temps n’influerait « que » sur le trajet de la pomme ? En effet, elle suit sa géodésique qui tient compte des déformations…?
Merci d’avance !
Bonjour Catherine,
(et désolé pour le retard)
En préambule…
Tout comme pour Philippe, dans la discussion précédente, la difficulté conceptuelle est normale, et très difficile à franchir tant elle contredit nos sens.
Je ne vais pas reprendre toute la discussion avec Philippe (lire ci-après) mais je vais tenter d’apporter une réponse rapide à vos deux points.
Aucune force ne s’exerce sur la pomme détachée (ou sur vous-même si vous étiez dans un ascenseur en “chute libre” : vous êtes toutes deux immobiles dans votre référentiel RG). Donc, non, rien “n’attire“ la pomme, et certainement pas une quelconque force électromagnétique. La force électromagnétique est à la base de ce que l’on appelle la résistance de l’air ou la résistance du sol lorsque la pomme ou vous, vous vous écraserez. Cette force est également à l’œuvre lorsque la tige empêchait la pomme d’être au repos, c’est-à-dire d’être en “chute libre”.
La difficulté conceptuelle est dans l’illusion de nos sens…
Lorsqu’un newtonien explique qu’un objet en mouvement rectiligne uniforme n’est soumis à aucune force (ou à des forces qui s’annulent), cela nous perturbe. On a tendance à se dire : je le vois avancer, c’est donc que quelque chose agit. Cela va contre nos sens, et pourtant cette relativité galiléenne est la base de la physique classique.
Et c’est pourquoi il nous est encore plus difficile de comprendre Einstein quand il nous dit qu’un objet en mouvement accéléré peut n’être soumis à aucune force (“chute” de la pomme). Et tout ceci vient d’une mauvaise interprétation par notre cerveau de ce qu’est l’espace et le temps ainsi que leur interaction (déformation de l’espace-temps) avec l’énergie (matière ou autre).
Ce n’est pas facile… Je sais 😉
Bonjour,
Une question concernant la pesanteur, j’ai cherché partout et n’obtient jamais de réponse très claire. La notion d’espace courbe et de géodésique reste assez intuitive, mais il reste un point qui n’est jamais abordé dans toutes les vulgarisations de la RG qui suit toujours le même schéma:
1- d’abord la description de la gravité Newtonienne, qui explique la pesanteur comme une force, et donc explique pourquoi une pomme tombe, tel le malheureux ouvrier de son échafaudage.
2- ensuite, en RG, la gravité n’est plus une force mais une déformation de l’espace, qui explique que les objets en mouvement suivent leur géodésique. Les exemples pris sont toujours les mêmes, c’est à dire des objets déjà en mouvement : la lune, le trajet des rayons lumineux
3- emporté (par l’inertie de son élan, probablement) le vulgarisateur enchaine sur les trous noirs, la matière noire, l’énergie noire, et bientôt les multivers, les branes et que sais-je encore. C’est passionnant mais
4- jamais on ne revient sur Terre pour ré-expliquer le point n°1 ci-dessus en termes non Newtionens: quid, en l’absence de force, de la mise en mouvement de la pomme qui tombe de l’arbre ?
Autrement dit, pourriez-vous expliquer en terme de RG ce qui fait qu’un objet qui ne tombe pas (parce qu’il est retenu par quelque chose) se met soudainement en mouvement si on supprime ce qui le retient, ce sans recourir à une force ? Peut-être que ça s’appelle (s’appelait ?) la pesanteur, je ne sais plus trop, mais enfin pourriez-vous en dire quelques mots en terme de RG. Merci.
Bonjour,
Tout d’abord merci pour votre question car je ne pense pas que vous soyez le seul, loin de là, à ressentir une difficulté à ce sujet.
En fait, une partie de l’article est consacrée à la réponse à cette question, et notamment ceci où vous pouvez remplacer votre personne par une pomme :
—-
De même, dans votre ascenseur en chute libre, vous n’êtes soumis à aucune force : vous suivez tout naturellement votre géodésique… qui, malheureusement pour vous, passe par le sol. Et si vous semblez accélérer, bien que vous ne ressentiez rien, c’est que votre géodésique suit la « courbure » appliquée à l’espace par la Terre. Vous parcourez plus d’espace par unité de temps parce que votre géodésique s’étire.
—-
Mais ce n’est sans doute pas assez explicite. Et vous me donnez l’occasion de (tenter de) réparer cela…
La difficulté vient du fait que vous continuez à raisonner en termes newtoniens. Or, les notions de référentiels galiléens, de mouvements rectilignes uniformes ont ici laissé place à la géométrie des géodésiques de l’espace-temps. Je m’explique, en commençant par la version newtonienne…
La pomme accrochée à l’arbre est soumise à deux forces en sens opposés qui s’annulent (la pesanteur et la réaction de l’arbre). Elle est comme un objet auquel aucune force ne s’applique et on peut lui faire correspondre un référentiel galiléen pour lequel elle est immobile. Un coup de ciseau, et Newton (et vous-même) dit qu’elle tombe. En effet, une seule force est à présent à l’oeuvre (la pesanteur, dirigée vers le bas), expliquant le mouvement accéléré du fruit vers le sol.
En RG, il en est tout autrement. Lorsque la pomme est attachée sur son arbre, une seule force est à l’oeuvre : celle qui fait que la pomme est attachée à l’arbre (résultant de la force électromagnétique entre chaque atome). Là où Newton la voit au repos, Einstein la voit constamment tirée vers le haut.
Inversement, après le coup de ciseau, Newton la voit soumise à la force de pesanteur, alors que pour Einstein, il n’y a plus de force en jeu : la pomme est au repos (tout comme l’homme “en chute libre” dans son ascenseur). C’est ici que cela bloque en général car vous avez de la difficulté à identifier la notion de “au repos” avec le mouvement de ce fruit qui va s’écraser sur votre tête.
Contrairement à ce qui est sans doute mal expliqué (et sans doute par moi-même), une géodésique n’est pas ici qu’une trajectoire, une géodésique décrit le comportement d’un objet au repos (un objet sur lequel aucune force n’est appliquée). Et ce comportement ne dépend que de la déformation de l’espace-temps (qui n’est pas qu’une déformation de l’espace) et de son mouvement propre, lui-même dépendant du référentiel RG choisi (et en RG, les référentiels ressemblent plus à des mollusques flasques qu’à ce que vous imaginez).
En le disant autrement, vous avez déjà fait un saut conceptuel si vous avez intégré les principes galiléens. Dans ce cadre, un objet qui suit une trajectoire rectiligne uniforme est au repos (il n’est soumis à aucune force ou à des forces qui s’annulent, ce qui revient au même). Ce simple concept est déjà choquant pour l’homme de la rue, que vous pouvez traduire par notre si trompeur “bon sens” : “si cela continue de bouger, c’est qu’il y a quelque chose qui le fait constamment bouger”.
Là, c’est un nouveau saut conceptuel que vous devez effectuer pour vous dire que la pomme qui “tombe” est en fait au repos, et que c’est le référentiel que vous utilisez inconsciemment qui vous trompe.
Merci pour votre réponse, sur laquelle je médite.
En effet, j’ai pu constater que je ne suis pas le seul à me poser cette question, et donc creuser la bonne manière de vulgariser la réponse n’est pas vain.
Vous avez bien compris là où ça coince: le moment du coup de ciseau qui libère la pomme.
Si je comprends bien (ce qui m’étonnerais un peu), à l’instar du mouvement rectiligne uniforme qui est « pour rien », en RG le mouvement accéléré du fait d’un champ de gravité est également « pour rien » pour le corps considéré qui est tout autant au repos (tant qu’aucune force ne vienne le dévier), c’est pour ça que la gravité en RG « n’est pas une force ». Ce sont « les observateurs » qui y voit une accélération. Est-ce que j’ai bon ?
Mais qu’est-ce qui fait que la pomme ne reste pas suspendue en l’air, là où elle est ?
Aïe, vous venez justement de me le dire: la fameuse géodésique. « une géodésique n’est pas ici qu’une trajectoire, une géodésique décrit le comportement d’un objet au repos (un objet sur lequel aucune force n’est appliquée). Et ce comportement ne dépend que de la déformation de l’espace-temps (qui n’est pas qu’une déformation de l’espace) et de son mouvement propre, lui-même dépendant du référentiel RG choisi »
Avant d’être libérée, la pomme n’a pas de mouvement propre (au moins par rapport au sol). Elle est dans une région de l’espace-temps qui reste ce qu’elle est, cette région ne se déforme pas. Donc le comportement de la pomme ne devrait pas être modifié. La seule chose qui change pour la pomme, c’est le temps qui passe, mais doit-on dire que la pesanteur est due au temps qui passe ? Pourquoi pas, ça ne me choquerait pas plus que ça mais je préfèrerais ne pas me mettre des idées trop fausses en tête.
Merci encore.
PS : Une chose encore, je n’ai pas bien compris comment interpréter l’expression « comportement d’un objet au repos ».
(Désolé pour le retard)
Dire qu’un objet est au repos, c’est une façon maladroite (mais j’assume) de dire qu’il n’est soumis à aucune force (ou à des forces qui s’annulent mutuellement).
Encore une fois, le blocage vient du fait que l’on raisonne en termes galiléens (ou pire en termes aristotéliciens). C’est ce qui s’exprime lorsque l’on dit : “Qu’est ce qui fait bouger la pomme ?”
Sinon, vous êtes tout à fait sur la bonne voie mais il reste quelques scories galiléens : “qu’est-ce qui fait que la pomme ne reste pas suspendue en l’air, là où elle est ?” ou encore “Avant d’être libérée, la pomme n’a pas de mouvement propre”.
D’un point de vue galiléen, la pomme accrochée est au repos. Un ami dans un train à vitesse constante, la verra se déplacer, elle et le pommier, d’une manière rectiligne et uniforme. Il est toujours possible de choisir un autre repère galiléen où elle paraîtra immobile : vous, allongé sous le pommier. Pas de difficulté.
Raisonnons maintenant autrement (RG). Je monte en haut d’un gratte-ciel avec une poire, et je saute dans le vide en lâchant le fruit. Faisons comme-ci il n’y avait pas de résistance de l’air. Qu’est ce que je constate ? Je semble flotter comme-ci je n’étais soumis à aucune force (et c’est le cas en RG). C’est également la même chose pour la poire à côté de moi. Je peux former une sorte de repère orthonormé avec ma tête et mes bras. Et je vous assure que la poire est bel et bien immobile par rapport à ce repère. Elle est au repos, tout comme moi. Ce n’est pas le cas de la pomme sur le pommier qui accélère dans ma direction et qui, elle, est donc soumise à une force. Mon repère peut vous sembler bizarre : il vous semble s’étirer au fil du temps. Mais ce n’est qu’un point de vue. Tout est réellement relatif en RG.
Quand vous dites “La pomme est dans une région de l’espace-temps qui reste ce qu’elle est, cette région ne se déforme pas.” C’est votre point de vue (qui est un peu faux d’ailleurs puisque cette région est déformée par tout ce qui l’entoure, et notamment la Terre). De mon point de vue (et celui de la poire) : je demeure dans une région de l’espace-temps qui reste ce qu’elle est mais qui est déformée par tout ce qui se déplace autour d’elle, et notamment par la Terre… qui vient vers moi un peu trop rapidement à mon goût.
Ma précédente réponse (à votre réponse du 25/04) n’apparait pas. Peut-être un problème technique, donc je réitère.
Une précision : j’ai volontairement circonscris ma question initiale à ce qui – dans la RG – crée ce que l’on appelle couramment la pesanteur par rapport à la conception newtonienne de force.
Vous m’avez répondu d’abord avec des rappels sur le mouvement rectiligne uniforme, et maintenant sur l’universalité de la chute libre. D’accord, mais je me permet de préciser que ce n’est pas ma question: en effet ces notions s’intègrent très bien dans un cadre newtonien, et donc que cela ne m’est d’aucune aide pour m’éclairer sur la spécifité de la RG versus Newton, objet de ma question.
Effectivement, je raisonne, la faute à mon parcours scolaire, très probablement en termes galiléens et newtoniens, et c’est bien pour ça que j’essaye de comprendre le raisonnement en RG pour ce qui concerne la pesanteur. Remarquez que vous n’y échappez pas non plus parfois, en disant « Ce n’est pas le cas [être au repos] de la pomme sur le pommier qui accélère dans ma direction et qui, elle, est donc soumise à une force ». C’est justement parce qu’il est dit que la pesanteur en RG n’est pas due à une force que je pose ma question. Si vous me parlez de force, là je n’ai plus de questions.
Dans votre message du 17/04, vous sembliez me répondre que la pesanteur est le résultat des déformations permanentes de l’espace-temps, et moi j’ai répondu que je ne voyais ces déformations comme permanentes et donc suffisantes pour expliquer la pesanteur (qui elle est permanente), en effet :
Je n’ai pas dit que la région où est la pomme n’est pas déformée par ce l’entoure. J’ai dit, ou voulu dire – pardon de mes imprécisions sémantiques – que selon la RG, cette région de l’espace-temps ayant acquis une forme (la résultante des influences gravitionnelles qui l’entourent) n’est ensuite pas déformée, de manière suffisament sensible évidemment. Autrement-dit, il n’y a pas de déformation sensible (j’insiste sur le mot « sensible ») des déformations.
J’ai bien conscience que l’espace-temps à un point de l’espace, et notamment celui de la pomme, est constamment déformé: les mouvements du noyau terreste, un oiseau qui passe, un quasar qui tousse. Mais en première approximation, il n’y a guère que la relation Terre-pomme dont il faille tenir compte, et là il n’y a pas de changements sensible (puisque vous avez parlé des déformations constantes comme étant la cause de la pesanteur) dans l’espace-temps de la pomme pour la mettre en mouvement.
Dans votre dernière réponse, je vous cite : « De mon point de vue (et celui de la poire) : je demeure dans une région de l’espace-temps qui reste ce qu’elle est mais qui est déformée par tout ce qui se déplace autour d’elle, et notamment par la Terre… qui vient vers moi un peu trop rapidement à mon goût.
A nouveau, la notion de déplacement/déformation intervient dans votre explication. Je n’ai rien contre, même si je trouve des déformations de déformation pas encore convaincantes, mais j’essaye de comprendre.
il serait plus simple raisonner avec une pomme théorique sur un arbre théorique sur une Terre théorique et homogène qui ne tourne pas. Je suppose que la RG prévoit tout de même des effets gravitationnels dans ces circonstances. Mais où sont ici les déformations dynamiques de l’espace-temps qui expliqueraient la pesanteur en l’absence de force? J’avais proposé le passage du temps, mais vous n’avez pas vraiment relevé l’hypothèse, donc ce n’est pas ça.
J’en suis pour l’instant à bien « voir » les déformations de l’espace-temps, mais si vous voulez, une fois déformé, je ne vois plus les déformations de la déformation, et donc je ne vois pas où serait la dynamique de la chose (et si vous me dites encore que je raisonne là en galiléen, je serais d’accord mais cela ne fait pas explication en soi: il vaut mieux consacrer plus de lignes à m’aider à raisonner maintenant en einsteinien)
Je voudrais préciser que je cherche pas à « contester » la RG, je n’en ai ni les moyens intellectuels, ni l’envie. J’ai beaucoup lu et beaucoup écouté sur ce sujet, et mon problème est que le point que j’aborde n’est tout simplement jamais évoqué. Je dirais même qu’il est évité, au moins dans la vulgarisation, et au mieux on se trouve renvoyé aux mathématiques pour en savoir plus: or, la RR et la mécanique quantique doivent être mathématiquement au moins aussi ardues, et pourtant on nous vulgarise sans problème des phénomènes autrement contre-intuitifs.
Pour la pesanteur, ça ne serait pas possible ? Newton parlait de force. J’aimerai comprendre comment le phénomène de pesanteur est expliqué en RG en s’affranchissant du concept de « force », cela me parait au coeur de la RG, et pourtant ce n’est jamais expliqué. J’ai pourtant l’impression que s’affranchir du terme « force » n’est pas une sorte de coquetterie, mais bien fondamental: pourquoi alors toutes les vulgarisations de la RG évitent soigneusement de vulgariser ce qui est fondamental à la théorie ? Puisque vous êtes membre du Café des sciences, peut-être quelqu’un là-bas pourrait venir me répondre ici ?
PS: pour se détendre, voici un lien vers 4 vidéos de Richard Taillet sur le sujet, http://www.scilogs.fr/signal-sur-bruit/weightless-2-apesanteur-et-chute-libre/
En réponse à Philippe…
Encore une fois, il n’y a aucune tare à raisonner en galiléen. L’école n’y est pour rien (si ce n’est au contraire d’avoir permis le passage du raisonnement aristotélicien au galiléen), ce sont nos sens qui sont trompés. Et si vous ne comprenez pas, la faute m’incombe en grande partie (l’autre partie étant due une fois encore à nos sens).
Cette difficulté (mauvaise vulgarisation + sens trompeurs) vous a, par exemple, fait croire que je parlais de l’universalité de la chute libre, alors qu’il s’agissait du contraire : j’essayais de vous expliquer que moi et ma poire, en RG, nous ne chutons pas puisque nous sommes au repos, sans qu’aucune force ne s’exerce sur nous. C’est vous, allongé sur l’herbe, ainsi que la pomme accrochée à l’arbre, qui êtes soumis à une force (et non deux qui s’annulent, comme pour Newton). Et la force dont je parle – contrairement à ce vous avez cru comprendre – n’a rien à voir avec la pesanteur. Elle est même dirigée dans l’autre sens. Vous ressentez d’ailleurs l’accélération causée par cette force, plaqué que vous êtes au sol comme si vous étiez dans une fusée accélérant vers le “haut” (et non vers le “bas” comme la pesanteur de Newton que votre corps ne ressent pas, ce qui a fait tiqué Einstein). Cette force, c’est ce que l’on appelle la force de réaction en termes newtoniens, et qui n’est autre que la résultante de la force électromagnétique repoussant chacun de nos atomes, y compris ceux de la Terre. Cette force s’oppose au fait que vous suiviez votre géodésique comme tout corps au repos (et c’est aussi ce qui ne va pas tarder à nous arriver à ma poire et à moi).
C’est ici que l’on arrive à votre questionnement. Qu’est qui fait que, moi et ma poire, nous suivons notre géodésique ? Ou, dans vos termes, qu’est ce qui met en mouvement la pomme lorsque vous donnez le coup de ciseau ?
Ces questions, agrémentées du petit topo précédent, peuvent d’ailleurs avoir comme corollaires d’autres questions que vous pouvez vous poser : puisqu’il n’y a qu’une force “vers le haut”, pourquoi n’êtes vous pas expulsé vers le ciel ? Et généralisé à la Terre, pourquoi n’explose t-elle pas ?
La réponse à toutes ces questions est : “Chaque atome de la Terre, chaque pomme, chaque poire suit (ou veut suivre) sa géodésique.”
Arrivé à ce stade de l’explication, je sais que vous n’avez qu’une envie : m’arracher les yeux. Et c’est humain : “Mais bon dieu, pourquoi ces corps veulent se déplacer sur cette foutue géodésique !? Et qu’est-ce qui les fait s’y déplacer, bordel !? C’est pourquoi – rassurez-vous – je vais poursuivre. Mais avant de le faire, il faut que je précise certaines choses…
1) Contrairement à ce que vous semblez croire (mais peut-être me trompe-je), la notion de force est présente en RG tout comme elle l’était chez Newton. Le principe est à peu près le même. On pourrait discuter du “à peu près” mais ça n’a pas grand intérêt ici. La vraie différence, c’est que la “force de pesanteur” n’existe pas en RG. Cela n’exclut en rien l’existence et la prise en compte d’autres forces qui, tout comme chez Newton, vont modifier le mouvement (dans sa direction et/ou sa vitesse), ceci dans un cadre (l’espace-temps de la RG) qui n’est toutefois pas le même que celui de Newton. Et je spoile un peu : il n’en reste pas moins qu’aucune force n’intervient dans le “déplacement” sur la géodésique.
2) Pour mon explication, je vais me servir d’exemples tirés de la physique de Newton et de la relativité galiléenne, non pas parce que vous ne comprenez rien à cette physique et qu’il faut vous l’expliquer mais, au contraire, parce que vous semblez bien la maîtriser et que je vais pouvoir m’appuyer sur vos acquis.
Ceci étant précisé, on y va !
Comme vous l’avez peut-être deviné, toutes ces questions peuvent se résumer en une seule : que signifie “suivre sa géodésique” ?
Et malheureusement, cette formulation est trompeuse. Je me permets d’entrer dans votre cerveau. Que voyez-vous dans “suivre sa géodésique” ?
Commençons par “sa géodésique”. Pour vous, c’est un chemin qu’emprunte un corps sur lequel ne s’exerce aucune force, un chemin biscornu car parcourant un espace-temps lui-même déformé par tout ce qu’il contient. C’est même plus qu’un chemin car il ne faut pas omettre la composante “temps”. La géodésique contient en elle l’information liée à l’accélération (ou la décélération) de l’objet sur ce chemin. C’est un peu comme si ce chemin, même en “ligne droite”, pouvait voir la distance entre ses bornes kilométriques s’étirer ou se contracter. On a coutume de représenter cela comme des montées et des descentes dans un univers représenté à plat (ce qui occasionne également bien des malentendus). C’est l’équivalent des trajectoires rectilignes uniformes chez Galilée, sauf qu’ici ces trajectoires sont tordues et étirées, au point même, parfois, de se recouper ou de se refermer sur elle-même.
Je pars du principe que vous avez intégré cela, même si cela n’est déjà pas évident pour nos sens.
Poursuivons avec “Suivre”. Et c’est ici que ce produit le blocage, intellectuellement parlant. Et ne soyez pas vexé, on y passe tous.
Pour comprendre la nature du problème, sachez qu’elle est exactement identique à celle qu’aurait un aristotélicien à qui vous essaieriez d’expliquer la nature galiléenne d’un mouvement rectiligne uniforme.
Imaginons qu’un train sur coussin d’air dont les moteurs ont été coupés, passe devant vous deux. L’aristotélicien va vous dire qu’il existe une force qui fait continuellement avancer ce train sur sa trajectoire, sinon il n’avancerait pas. C’est du bon sens. Pourtant, vous aurez à lui expliquer (et je vous laisserai le faire) qu’aucune force ne fait avancer son train. D’ailleurs, dans ce cadre, une personne dans le train peut tout à fait se dire immobile. Il constate que votre duo de penseurs et le pommier sous lequel vous êtes abrités, se déplacent dans un mouvement rectiligne uniforme. Et aucune force n’est responsable de ce déplacement. Pourtant, pour ce voyageur, vous êtes en train de vous déplacer sur un chemin (une ligne droite) qu’il peut parfaitement dessiner. Pour lui, vous suivez votre géodésique galiléenne.
Il en est de même en RG. C’est maintenant à moi d’expliquer à mon ami galiléen (vous) pourquoi la pomme suit sa géodésique (ce qui n’a plus rien d’un mouvement rectiligne uniforme) sans qu’aucune force ne soit en jeu.
Restons dans le monde galiléen. Vous parlez à votre ami de cette pomme accrochée à l’arbre, et qui, pour vous comme pour le voyageur, est au repos (elle n’est soumise à aucune force ou à des forces qui s’annulent). Mais votre ami aristotélicien qui s’ennuie a, entretemps, sorti son trampoline. Et au moment où vous lui parlez de cette pomme, il la regarde alors qu’il est en train de sauter. Revenu sur le plancher des vaches, il vous assure qu’il a vu cette pomme se diriger vers le bas avec un mouvement accéléré.Vous lui expliquez que le repère qu’il a choisi pour analyser le mouvement de la pomme n’était pas le plus heureux. Et vous lui parlez des repères galiléens : à chaque corps au repos (la pomme ou le train) vous pouvez faire correspondre un repère galiléen pour lequel ce corps sera immobile. Or dans le repère choisi par votre ami lors de son saut, aucun corps au repos ne peut paraître immobile. Ce n’est donc pas un repère galiléen. Ce qu’il a vu n’était pas une illusion mais le trompe sur la nature des forces en présence.
Quittons le monde galiléen.
A quoi ressemble la géodésique de la poire (et de moi-même) selon vous qui êtes allongé sur l’herbe. Pour la dessiner, imaginons que je puisse traverser la Terre sans résistance. Cela ressemble à un segment de droite (en fait, une ellipse totalement aplatie) que je parcours en accélérant jusqu’au centre de la Terre avant de décélérer jusqu’à m’immobiliser de l’autre côté de la terre, et de refaire le chemin en sens inverse, et ceci continûment. Et vous vous demandez qu’est-ce qui peut bien me faire parcourir ce chemin puisque la pesanteur n’existe pas en RG.
Mais cela, c’est votre vision à vous, selon votre repère. Et encore une fois, c’est le repère que vous avez choisi qui trompe votre cerveau.
J’ai un autre repère à vous proposer : celui que je forme avec mes bras et ma tête autour de la poire. Or aucune force n’agit sur moi et la poire. Je suis donc au repos. Et de plus, dans ce repère je suis immobile. Je pourrais donc dire que c’est un peu l’équivalent dans le monde einsteinien d’un repère galiléen. Enfin, uniquement dans le sens où ce repère me permet de parfaitement comprendre les forces en jeu autour de moi.
Je peux également vous dire à quoi ressemble ma géodésique selon ce si intéressant repère en RG : elle ressemble à un point. Moi et ma poire, nous sommes parfaitement immobiles. Cela relativise beaucoup ce que l’on peut entendre par “suivre sa géodésique”.
En revanche, Dans le repère que vous avez choisi, au sol, pour étudier tout cela, rien ne va plus. Dans ce repère, (et je précise) autour de vous, vous ne pourrez trouver aucun corps au repos (voir la définition) qui soit immobile. Votre repère ne vaut pas mieux que celui de votre ami sur le trampoline. Et c’est ce qui vous trompe.
Bon, je dois quand même préciser que j’abuse un peu concernant ces repères, et que je peux induire de fausses idées. Contrairement au monde galiléen, en RG, tous les repères se valent (dont le G de RG). Dans le vôtre, par exemple, un corps au repos peut être immobile. Mais il se situe, en première approximation au centre de la Terre. C’est pourquoi je précisais “autour de vous”.
Revenons au point de départ.
En RG, la pomme attachée à l’arbre n’est pas au repos. Une force (et non deux) agit sur elle (vers le haut). C’est quand vous donnez le coup de ciseau qu’elle redevient au repos. De son point de vue, elle redevient même immobile. Pour les autres repères, elle se remet à suivre une géodésique dont la forme dépendra du repère choisi. Vous avez l’équivalent dans le monde de Newton avec un train dont on coupe le moteur. Il se remet à suivre une trajectoire rectiligne uniforme avec une direction et une vitesse qui dépendent du repère galiléen choisi.
La vraie difficulté est de comprendre cette accélération vers le haut. Et pourtant vous-même, allongé dans l’herbe, vous la ressentez dans chaque partie de votre corps. Fermez les yeux, et vous pouvez sans mal vous imaginer plaqué au sol, dans une fusée accélérant vers le haut.
Dès lors, pourquoi vous ne quittez pas le sol ? Pourquoi la Terre n’explose t-elle pas ? C’est qu’il faut prendre en considération la notion de courbure de l’espace-temps qui, elle-même, vient influer sur la nature de votre géodésique. Vous accélérez réellement vers le haut, vous vous déplacez en accélérant vers le haut mais uniquement par rapport au repère correspondant à votre immobilité sur votre géodésique. Ici, c’est le repère qui compte, celui qui vous permet de comprendre ce qu’il se passe. Imaginez que le sol se dérobe sous vous. Vous voilà immobile sur votre géodésique, vous ne ressentez plus aucune force, et que voyez vous : un pommier et sa pomme attachée qui accélèrent vers le haut.
Enfin bref, voilà, j’ai fait de mon mieux. En espérant de tout cœur que mes efforts aient été suffisants. Sinon désolé. Bonne continuation en tout cas dans l’espace-temps 😉
Merci pour tout le temps que vous avez pris pour tenter de m’expliquer.
Il est effectivement temps de mettre fin à cet échange, car vous n’avez pas ménagé vos efforts, je vous en remercie, et donc maintenant la balle est dans mon camp. Bonne continuation à vous également.