La Relativité (3) : ça se contracte

Après qu’on ait cherché un centre absolu au centre de la Terre, puis au centre du Soleil, la relativité des lois physiques, donc sans le recours au moindre repère absolu, va peu à peu s’imposer dans la nouvelle culture scientifique des XVII^e et XVIII^e siècles. Mais dans le courant du XIXe siècle, l’évidence va laisser place au doute pour finalement aboutir au retour de l’absolutisme. Voyons cela de plus près…

La Relativité s’éclaire

Pour la suite de notre histoire, l’Église va se retirer du débat sur la pointe des pieds, et, sur les pas de Galilée, nombreux sont ceux qui vont construire, peaufiner et renforcer le nouveau cadre dans lequel s’inscrit l’univers, avec en premier lieu un certain Isaac Newton, dans l’Angleterre de la fin du XVII^e siècle (jolie perruque ci-dessous). Là encore, nous allons faire l’impasse sur nombre de ses collègues, et sur beaucoup de choses concernant ce drôle de monsieur né quelques mois après la mort de Galilée.
En gros, disons qu’avec sa Loi de l’attraction universelle (la gravitation), Isaac Newton va mettre en équations les mouvements des astres (et des pommes). Et tous les centres absolus ont disparu. Avec ses Lois de la Mécanique (rien à voir avec votre voiture), l’univers est désormais régi par les forces et les mouvements, et c’est le triomphe de la Relativité.

En effet, toutes les lois de la nature s’expriment désormais de façon identique quel que soit le repère (ou référentiel) choisi. Vous vous souvenez : un référentiel, c’est ce petit point zéro (l’origine) muni de ses trois flèches (les axes).
Un petit bémol toutefois : ceci n’est vrai que pour les « référentiels galiléens », également appelés « référentiels inertiels »…
Qu’est-ce que c’est que cette bête ? Pour faire simple, c’est un référentiel qui n’est pas soumis à une accélération… ou à un freinage qui, en physique, n’est qu’une accélération négative… ou à une rotation qui n’est qu’une accélération dont la direction varie. Enfin bref, un référentiel qui semble immobile ou dans un mouvement rectiligne (tout droit) uniforme (sans variation de vitesse). Une façon plus newtonienne de le dire est que, dans un tel référentiel, tout corps libre (sur lequel ne s’exerce aucune force ou sur lequel la résultante des forces est nulle) est en mouvement de translation rectiligne uniforme ou au repos (qui n’est qu’un cas particulier de mouvement rectiligne uniforme). Mais bon,  le fait est là : tous ces référentiels se valent.

Allez, un peu de chloroforme pour mieux comprendre…
Vous vous réveillez enfermé dans une pièce sans fenêtre, insonorisé, un container, un laboratoire avec tous les instruments de mesure possible. Deux possibilités : votre container est soit immobile en gare, soit il se déplace à vitesse constante sur un train à coussin d’air. Et je vous demande de déterminer quelle est votre situation ? Train en marche ou à l’arrêt ?…
La réponse est simple : vous ne pouvez pas !
Toutes les expériences que vous mèneriez donneraient un résultat identique que vous soyez dans la gare ou dans le wagon. Lâchez un poids (par sécurité, prenez une pomme), il tombera sur votre pied quelle que soit votre situation… Les Lois s’appliquent de façon identique, sans que soit privilégié tel ou tel référentiel. On peut toujours dire que l’on est mobile ou immobile par rapport à quelque chose (un référentiel) mais cela n’a plus de sens de dire que l’on est mobile ou immobile de manière absolue. C’est ça, la Relativité.

Précisons que l’exemple du container que je vous ai donné, était présent dans le « Dialogue sur les deux grands systèmes du monde » de Galilée (à part qu’il s’agissait de la cabine d’un bateau), ce qui lui avait permis d’écrire : « le mouvement, c’est comme rien »… Mais c’est bien Newton qui va formaliser tout cela. Et ses équations vont se révéler méga efficaces, aussi bien pour les planètes que pour les obus… ou les pommes.

La lumière assombrit la Relativité

Alors que la Mécanique newtonienne triomphe, des progrès vont peu à peu être effectués quant à la compréhension de trois phénomènes physiques a priori distincts : l’électricité, le magnétisme et la lumière. Des progrès qui vont aboutir à la réunion de ces trois éléments dans ce que l’on allait appeler l’électromagnétisme. Nous allons à nouveau mettre de côté de nombreux personnages pour nous concentrer sur celui qui est ici à la baguette : un mathématicien et physicien écossais, James Clerk Maxwell (jolie barbe ci-dessous). On est alors en 1861 et, tout comme Newton deux siècles plus tôt, il va nous pondre un chef d’œuvre avec ses bien nommées « Équations de Maxwell ».

Deux forces fondamentales étaient alors connues : la gravitation et la force électro-magnétique. Si la première semblait parfaitement décrite par Newton, la seconde venait, avec ces équations, de trouver son cadre théorique. Un cadre alors en parfait accord avec l’expérimentation mais dont les conséquences allaient provoquer bien des migraines.

De fait, ces équations confirmaient (à l’époque) que la lumière était une onde, désormais nommée onde électromagnétique (ci-dessous une représentation de cette onde électromagnétique, si ça vous fait plaisir). Tout comme la vague est une onde se propageant sur l’eau, ou tout comme le son est une onde se propageant dans l’air, il fallait bien quelque chose, un milieu au sein duquel se propageait la lumière. Ce « quelque chose », on allait l’appelait « l’éther luminifère ». Rien à voir avec le produit chimique qui embrume les esprits… quoique la sensation était ici très proche pour les esprits scientifiques. En effet, cet éther devait avoir des caractéristiques bien étranges, pour ne pas dire contradictoires.

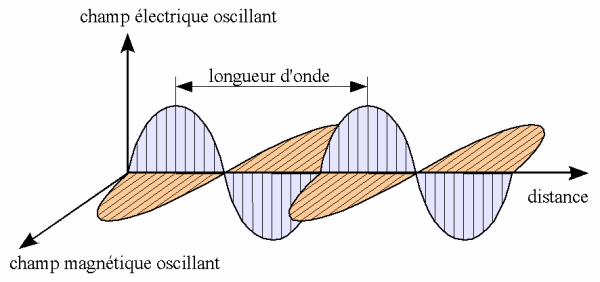
Premièrement, cet éther devait être assez rigide pour permettre à la lumière de se propager sur de très très très longues distances sans être trop atténuée en route (et nous permettre ainsi de voir les étoiles). Toutefois, cet éther bien rigide devait quand même être assez élastique pour vibrer, et surtout il ne devait opposer quasiment aucune résistance au déplacement de la matière en son sein car sinon, cela aurait été détecté : les Lois de Newton auraient été prises à défaut, les planètes et les obus étant freinés par l’éther. Donc, rigide, élastique et sans résistance au mouvement des objets. Bizarre, non ?

Mais le pire est encore à venir. Cet éther luminifère, semblant baigner tout l’univers, devait de plus être… immobile. Oui, les équations de Maxwell venaient de recréer ce que l’on avait eu tant de mal à faire disparaître : un référentiel absolu, par rapport auquel on peut dire que telle ou telle chose est mobile ou immobile. Nous voilà bien…

Concrètement, visualisons un champ électrostatique, c’est à dire la description dans l’espace des effets d’un phénomène électrostatique. Imaginez des tas de petites flèches pointant vers le centre ou l’extérieur, groupées en boule, et représentant la force qui s’exerce en chaque point de l’espace. Eh bien, selon ce nouveau cadre théorique, ce champ va s’écraser dans le sens du mouvement, et ce d’autant plus que vous vous déplacerez vite par rapport à l’éther (schéma ci-dessous).

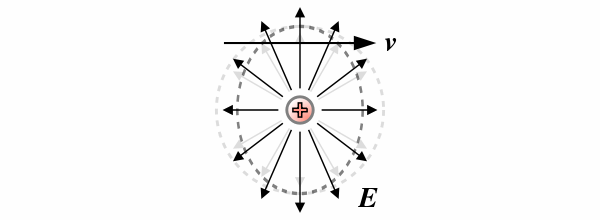
Vous vous souvenez du container dans lequel vous étiez enfermé. Il vous suffit donc maintenant d’étudier un champ électrostatique pour connaître non seulement de combien vous êtes en mouvement par rapport à l’éther mais en plus quel est l’axe de ce mouvement, et ainsi déterminer votre situation !

Vous l’avez compris : la Relativité semble ici bien moribonde.

La lumière montre la voie

C’est alors qu’une nouvelle expérience va tout à la fois interloquer le monde scientifique et fournir une piste pour sauver ce qui peut être sauvé de la Relativité. Allez, je me permets un petit spoiler : ce sera une « presque » fausse piste car elle mènera bien près de la solution. Le bon chemin sera emprunté lors de l’année miraculeuse de 1905 et, je vous rassure, la Relativité sera plus que sauvée !

Mais revenons à notre expérience… Il s’agit en fait d’une série d’expériences menées par deux physiciens américains, Albert Michelson et Edward Morley, entre 1881 et 1887 (jolies moustaches ci-dessous). Il s’agissait de déterminer les variations de la vitesse de la lumière selon la rotation de la Terre autour du Soleil (ou, si vous préférez, le mouvement de la Terre dans l’éther luminifère).
C’est assez simple à comprendre. Imaginez-vous, l’été, quittant la plage pour nager vers l’océan. Vous allez dans le sens contraire des vagues, et vous constatez donc qu’elles vous arrivent très vite dessus, à un rythme soutenu. En revanche, lorsque vous reprenez la direction de la plage, les vagues continuent de vous dépasser mais, par rapport à vous, bien plus lentement qu’avant.
En cette fin de XIXe siècle, les ondes lumineuses ne sont rien d’autre que des vagues d’éther. Et la Terre est un peu comme ce nageur. Il s’agit donc de mesurer la vitesse de ces vagues par rapport à la Terre, et plus exactement la variation de cette vitesse selon que la Terre va dans un sens ou dans le sens opposé, six mois plus tard, le long de son orbite.

Et après six ans de mesures faites et refaites, il a bien fallu se rendre à l’évidence : quelles que soient la vitesse et la direction de la Terre par rapport à l’éther, la vitesse de la lumière ne varie jamais. C’est a priori incompréhensible.

Prenons un autre exemple pour bien comprendre. Dans un train roulant à 100km/h, un enfant lance dans la rangée centrale un ballon à 10km/h. Si vous êtes sur le quai et que vous voyez passer le train, vous pouvez mesurer la vitesse du ballon. Si celui-ci est envoyé vers l’avant du train, vous mesurerez une vitesse du ballon de 110km/h (vitesse du train + vitesse du ballon dans le train). S’il est envoyé vers l’arrière, vous mesurerez 90km/h (vitesse du train – vitesse du ballon dans le train). Et si l’enfant est un prodige et shoote très fort, à 100km/h, vers l’arrière du train, vous aurez même l’impression que le ballon reste immobile devant vous alors que le train avance. Cela s’appelle la composition galiléenne des vitesses, et c’est très simple à comprendre (vous avez dû faire des exercices de ce type à l’école).
Maintenant, imaginez que cet enfant ait une lampe électrique. Quand il l’allume, on peut mesurer dans le train que la lumière s’en échappe à une vitesse très grande mais néanmoins finie que l’on va nommer « c ». Vous qui êtes sur le quai, vous allez également essayer de mesurer la vitesse de cette lumière. Si le faisceau est orienté vers l’avant du train, vous devriez, en toute logique, trouver une vitesse de c + 100km/h. Et si orienté vers l’arrière du train, une vitesse de c – 100km/h…
Sauf que non… Tout comme dans l’expérience de Michelson-Morley, vous allez obtenir « c ». La même vitesse que celle mesurée dans le train. Alors que vous êtes sur le quai et que la torche, dans le train, passe devant vous à 100km/h…

En fait, même si vous vous lanciez à la poursuite de cette lumière sortant de la lampe du gamin, dans une fusée Klingon allant presque à la vitesse de la lumière, histoire de l’observer passer au ralenti comme si, en voiture, vous suiviez des chevaux de course… Eh bien ce serait raté : la lumière passerait devant vous, à nouveau, à une vitesse égale à « c ». Incompréhensible… Ou presque.

La presque fausse piste

Devant ce résultat, certains émirent une hypothèse pas si saugrenue que ça. Voici ce que cela donne… en gros.
Puisque le champ électrostatique se contracte dans le sens du mouvement (par rapport à l’éther), imaginons que toute la matière soit constituée d’atomes (l’existence de l’atome n’était alors pas encore prouvée) et imaginons également que ces atomes soient tenus entre eux par quelque chose qui a à voir avec l’électromagnétisme. Dès lors, on peut concevoir que si ces atomes sont en mouvement (par rapport à l’éther), ils vont se resserrer dans le sens du mouvement. Et comme ces atomes concernent aussi bien votre propre personne que les instruments de mesure et le mètre-étalon (qui donc se rétractent aussi), cela pourrait expliquer le résultat négatif de l’expérience Michelson-Morley. Et en y regardant de plus près, ce n’est pas faux.

Dans cette hypothèse, la vitesse de la lumière est « c » si vous êtes immobile par rapport à ce repère absolu qu’est l’éther. Si vous vous déplacez, alors, conformément à Galilée, la vitesse de la lumière pour vous ne sera plus « c »… mais vous apparaîtra quand même égale à « c » car vos instruments de mesure et vous-même, et votre vaisseau ou votre Terre, seront contractés de telle sorte que l’illusion sera parfaite.

Plusieurs hommes vont formaliser cette illusion, cette contraction de la matière due à l’interaction de celle-ci avec l’éther. Une illusion qui devait aussi jouer sur la façon de mesurer le temps. Ce sera principalement le cas du physicien néerlandais Hendrik Lorentz (ci-dessus). Ses travaux seront repris et améliorés par le Français Henri Poincaré (ci-dessous). Ce dernier livrera des équations de transformation – qu’il nommera de manière chevaleresque « transformations de Lorentz » – permettant de calculer exactement l’effet de ces contractions selon les référentiels choisis.

Pour tout dire, quand on lit ses commentaires, que l’on comprend sa méfiance vis-à-vis des notions d’espace et de temps absolus, et que l’on sait l’importance que vont avoir ses « transformations de Lorentz », Poincaré est vraiment à un chouia d’ouvrir la bonne porte. Mais il faut se rendre à l’évidence, cette porte, il ne la voit pas, aveuglé qu’il est – comme toute la communauté scientifique – par cet éther et son référentiel absolu. Et si cette porte demeure invisible, c’est aussi parce que, pour l’apercevoir, il faudrait pour cela détruire des pans entiers de notre connaissance intime du monde, de ce que nous avons toujours tenu pour évident depuis la nuit des temps.

Sans doute fallait-il l’insouciance de la jeunesse pour la voir, cette porte. En 1905, un jeune homme inconnu, modeste employé d’un Office des brevets à Berne, la vit… et l’ouvrit.

La relativité

• Partie 1 : ce n’est pas absolu
• Partie 2 : c’est l’égalité
• Partie 3 : ça se contracte
• Partie 4 : c’est révolutionnaire
• Partie 5 : c’est aussi « E= mc² »
• Partie 6 : c’est général